Geometrische Deutung der partiellen Ableitung

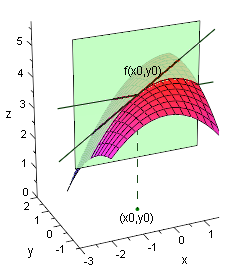
PaDeut.png
Sei f(x,y)f(x,y) eine Funktion, die von zwei Variablen abhängt. Ist ff im Punkt (x0,y0)(x_0,y_0) partiell differenzierbar, so können wir analog zu den reellen Funktionen die partielle Ableitung als Anstieg einer Tagente deuten.
Wir wollen ∂f∂x\dfrac{\partial f}{\partial x} betrachten. Dazu legen wir durch (x0,y0)(x_0,y_0) eine Ebene, die parallel zur x,zx,z-Ebene ist (also der Gleichung y=y0y=y_0 genügt). Die partielle Ableitung ∂f∂x(x0,y0)\dfrac{\partial f}{\partial x}(x_0,y_0) ist nun genau der Anstieg einer Tangente an die Fläche durch f(x0,y0)f(x_0,y_0), die in dieser Ebene liegt.
Bilden wir den Durchschnitt der Fläche des Graphen der Funktion mit der Ebene, so erhalten wir eine Kurve. Die partielle Ableitung entspricht dem Anstieg der Tangente in f(x0,y0)f(x_0,y_0) an diese Kurve.
 
 

Das entscheidende Kriterium ist Schönheit; für häßliche Mathematik ist auf dieser Welt kein beständiger Platz.

Godfrey Harold Hardy

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Differentiation