Metriken im Euklidischen Raum

Für den $\domRn$ können wir verschiedene Metriken definieren

$d_2( x,y):=\sqrt{\sum\limits_{i=1}^n (x_i-y_i)^2}$

Hierbei handelt es sich um die euklidische Metrik.

Die ersten beiden Eigenschaften verifiziert man leicht. Die Dreiecksungleichung folgt aus der Cauchy-Schwarzschen Ungleichung.

$d_\infty(x, y):=\max_{i=1\, \, \, n} |x_i-y_i|$

Diese Metrik heißt Maximummetrik.

Die ersten beiden Eigenschaften sind trivial nachzuweisen. Bleibt die Dreiecksungleichung. Zu zeigen ist $\max_{i=1\, \, \, n} |x_i-y_i|\leq \max_{i=1\, \, \, n} |x_i-z_i|+\max_{i=1\, \, \, n} |z_i-y_i|$. Das Maximum auf der linken Seite muss für einen Index $k$ angenommen werden. Für dieses $k$ gilt aber die Ungleichung $|x_k-y_k|\leq |x_k-z_k| + |z_k-y_k|$. Dies ist wiederum kleiner als das Maximum auf der rechten Seite, womit sich die Behauptung ergibt.

$d_1( x, y):=\sum\limits_{i=1}^n |x_i-y_i|$

Einziger Problemfall ist wieder die Dreieckungleichung. Diese ergibt sich aber sofort, da sie hier nur eine endliche Aufsummation der Dreiecksungleichung für reelle Zahlen ist.

Für $p\ge 1$ können ganz allgemein eine Metrik

definieren. Der Nachweis der Metrikeigenschaften ist bis auf die Dreiecksungleichung wieder relativ trivial. Die Dreiecksungleichung entspricht aber in diesem Fall der Minkowskischen Ungleichung.

Unter den "Einheitskugeln" $E_d$ unter den obigen Metriken versteht man die Mengen aller Punkte mit einem Abstand von höchsten 1 vom Ursprung $E_d=\{x\in\domRn |d(x,0)\leq 1\}$.

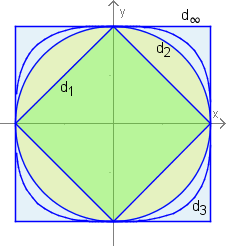
Für die euklidische Metrik handelt es sich dabei auch um Kugeln im geometrischen Sinn. Bei der Maximummetrik um Würfel um den Ursprung mit der Kantenlänge 2.

Die Grafik zeigt die Einheitskugeln (Einheitskreise) im ${\domR}^2$ für die einzelnen Metriken.