Elliptische Koordinaten

Im elliptischen Koordinatensystem wird ein Punkt durch Angabe der Lage auf konfokalen Ellipsen und Hyperbeln bestimmt.
Bei zweidimensionalen elliptischen Koordinaten lautet die Umrechnung in kartesische Koordinaten
r=(xy)=C⋅(cosh⁡(u)⋅cos⁡(v)sinh⁡(u)⋅sin⁡(v))\vec r=\begin{pmatrix} x \\ y \end{pmatrix} = C \cdot \begin{pmatrix} \cosh(u) \cdot \cos(v) \\ \sinh(u) \cdot \sin(v) \end{pmatrix}
u und v sind hier die Koordinaten, C ist ein Parameter des Koordinatensystems. v läuft von 0 bis 2π\pi, u ist nicht beschränkt (jedoch ist bereits mit den positiven Werten für die Beschreibung der gesamten Ebene ausreichend und eindeutig!). Die u-Koordinatenlinien sind Hyperbeln, die v-Koordinatenlinien Ellipsen; für u=0 ist die v-Koordinatenlinie zu einer Strecke von (−C0)\begin{pmatrix} -C \\ 0 \end{pmatrix} bis (C0)\begin{pmatrix} C \\ 0 \end{pmatrix} entartet, für v=0 ist die u-Koordinatenlinie zu einer Halbgerade entartet, der positiven x-Achse ohne der vorher erwähnten Strecke entspricht, für v=π\pi ist die u-Koordinatenlinie die entsprechende Halbgerade auf der negativen x-Achse und für v=π\pi/2 und v=3π\pi/2 ist die u-Koordinatenlinie die y-Achse.
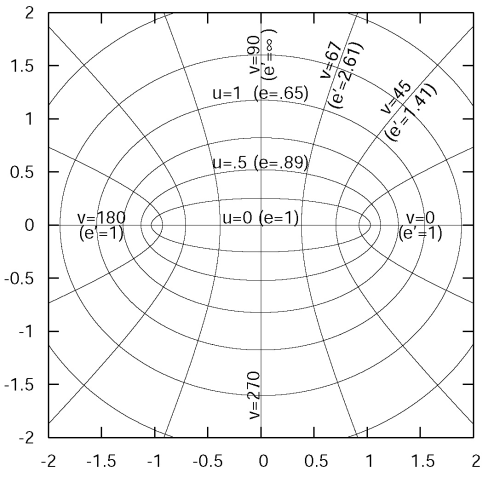
EllKoor.png
Elliptische Koordinaten in der Ebene für C
Alle Ellipsen und Hyperbeln haben die gleiche lineare Exzentrizität ae=C, wobei a die große Halbachse der Ellipse bzw. Hyperbel ist. Die lineare Exzentrizität einer Ellipse, auf der u=const ist, ist e=1/coshu. Die lineare Exzentrizität einer Hyperbel, auf der v=const ist, ist e=1/cos⁡ve=1/\cos v .
Diese elliptischen Koordinaten können auf verschiedenen Arten auf den dreidimensionalen Raum erweitert werden. Bei zylindrischen elliptischen Koordinaten wird einfach die kartesische z - Koordinate als weitere Koordinate hinzugefügt. Bei polaren elliptischen Koordinaten wird die Ebene um einen Winkel θ\theta gedreht, der dann die zusätzliche Koordinate bildet:
r(xyz)=C⋅[cosh⁡(u)⋅cos⁡(v)⋅(100)+sinh⁡(u)⋅sin⁡(v)⋅(0cos⁡(θ)sin⁡(θ))]\vec r\begin{pmatrix} x \\ y \\ z \end{pmatrix} = C \cdot \ntxbraceL{\cosh(u) \cdot \cos(v) \cdot \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} + \sinh(u) \cdot \sin(v) \cdot \begin{pmatrix} 0 \\ \cos(\theta) \\ \sin(\theta) \end{pmatrix}}
Schließlich gibt es noch räumlich elliptische Koordinaten:
r(xyz)=C⋅[cosh⁡(u)⋅cos⁡(v)⋅(100)+sinh⁡(u)⋅sin⁡(v)⋅(0cos⁡(θ)b⋅sin⁡(θ))]\vec r\begin{pmatrix} x \\ y \\ z \end{pmatrix} = C \cdot \ntxbraceL{\cosh(u) \cdot \cos(v) \cdot \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} + \sinh(u) \cdot \sin(v) \cdot \begin{pmatrix} 0 \\ \cos(\theta) \\ b \cdot \sin(\theta) \end{pmatrix}}
Hier ist b ein weiterer Parameter des Koordinatensystems. Die θ\theta-Koordinatenlinien sind hier Ellipsen. v läuft hier von 0 bis π\pi, u von 0 bis unendlich und θ\theta von 0 bis 2π\pi.
 
 

Jede Wissenschaft bedarf der Mathematik, die Mathematik bedarf keiner.

Jakob I. Bernoulli

Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel Elliptische Koordinaten aus der frеiеn Enzyklοpädιe Wιkιpеdιa und stеht unter der Dοppellizеnz GNU-Lιzenz für freie Dokumentation und Crеative Commons CC-BY-SA 3.0 Unportеd (Kurzfassung). In der Wιkιpеdιa ist eine Listе dеr Autorеn des Originalartikels verfügbar. Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Analytische Geometrie