Verteilung der Primzahlen und Primzahlsatz

Der Primzahlsatz sagt, dass sich die Anzahl der Primzahlen für großes xx annähernd wie xln⁡x\dfrac x {\ln x} verhält und erlaubt damit eine Abschätzung der Verteilung der Primzahlen.

Die Primzahlfunktion

Wir definieren π(x)\pi(x) als die Primzahlfunktion, die für beliebige reelle Zahlen xx definiert ist und die Anzahl der Primzahlen p≤xp\leq x zurückgibt. Formal:
π(x)=#{p∈P∣p≤x}\pi (x) = \# \{p \in \mathbb{P} \mid p \le x\} ,
wobei P\mathbb{P} für die Menge der Primzahlen steht und #M\#M für die Anzahl der Elemente der Menge MM.

Der Primzahlsatz

Der Primzahlsatz besagt:
lim⁡x→∞π(x)xln⁡(x)=1 \lim_{x \to \infty}\dfrac{\pi(x)}{\dfrac{x}{\ln(x)}} = 1\,
Die Funktionen π(x)\pi(x) und x/ln⁡xx/{\ln x} sind also asymptotisch äquivalent.

Stärkere Formen des Primzahlsatzes

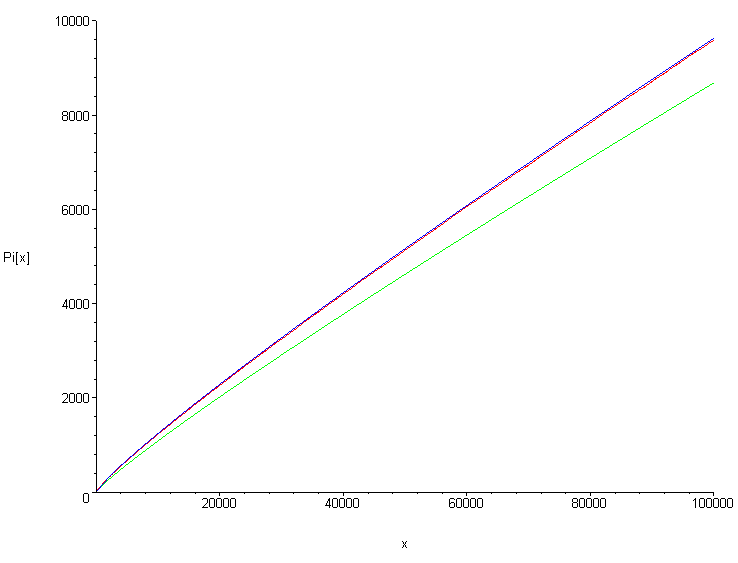
PrimeNumberTheorem.png
Darstellung von π\pi(x) (blau), xx / ln(x) (grün) und Li(x) (rot)
Bessere Approximationen als x/ln⁡xx /{\ln x} liefert der so genannte Integrallogarithmus, der definiert wird als
Li(x):=∫2xdtln⁡t  \mathrm{Li}(x) := \int\limits_2^x \dfrac{\mathrm{d}t}{\ln t}\,
(Die Integraldarstellung für Li(x)\mathrm{Li}(x) wird gewählt, weil die Stammfunktion von 1/ln⁡(x)1/\ln(x) nicht elementar ist.)
Der Integrallogarithmus ist asymptotisch äquivalent zu x/ln⁡xx/{\ln x}, also auch zu π(x)\pi(x).
Man kann sogar zeigen:
π(x)=Li x+O(x⋅exp⁡(−Cln⁡x))\pi(x) = \mathrm{Li}\,x + \mathcal O \left(x \cdot \exp(-C\sqrt{\ln x} )\right)
mit einer positiven Konstanten CC. O(⋅)\mathcal{O}(\cdot) ist dabei ein Landau-Symbol, d.h., es gibt eine Konstante DD, so dass
∣π(x)−Li x∣ < D⋅x⋅exp⁡(−Cln⁡x)|\pi(x)-\mathrm{Li}\,x | \ <\ D\cdot x \cdot \exp \left(-C\sqrt{\ln x} \right)
für alle xx gilt.
Das bedeutet, dass die Anzahl der Primzahlen, die kleiner als xx sind, anhand der Funktion xln⁡(x)\dfrac{x}{\ln(x)} abgeschätzt werden kann. Genauer gesagt: Man weiß, dass die Anzahl der Primzahlen, die kleiner als xx sind, größer ist als der Wert xln⁡(x)\dfrac{x}{\ln(x)}, wobei die verhältnismäßige Differenz mit zunehmendem xx geringer wird. Zum Beispiel folgt daraus, dass es mehr als 100000ln⁡(100000)=8685,89\dfrac{100000}{\ln(100000)} = 8685,89, also mehr als 8685 Primzahlen unter den ersten 100000 Zahlen gibt.
Unter Annahme der Riemannschen Vermutung, und nur unter dieser, kann man die Fehlerabschätzung zu
π(x)=Li x+O(x⋅ln⁡x)\pi(x) = \mathrm{Li}\,x + \mathcal O \left(\sqrt{x} \cdot \ln x \right)
verbessern.

Siehe auch

 
 

Wir Mathematiker sind die wahren Dichter, nur müssen wir das, was unsere Phantasie schafft, noch beweisen.

Leopold Kronecker

Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel Primzahlsatz aus der frеiеn Enzyklοpädιe Wιkιpеdιa und stеht unter der Dοppellizеnz GNU-Lιzenz für freie Dokumentation und Crеative Commons CC-BY-SA 3.0 Unportеd (Kurzfassung). In der Wιkιpеdιa ist eine Listе dеr Autorеn des Originalartikels verfügbar. Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Elementare Zahlentheorie