Symmetrische Gruppe S4

Die symmetrische Gruppe S4\bm{S_4} besteht aus 24 Elementen, den Permutationen einer vierelementigen Menge. Im folgenden eine Übersicht über die Ordnungen und Typen von Elementen.
Ordnung Signum Anzahl Permutationen
1 +1 1 (1)
2 -1 6 (12); (13); (14); (23); (24); (34)
2 +1 3 (12)(34); (13)(24); (14)(23)
3 +1 8 (123); (132); (124); (142); (134); (143); (234); (243)
4 -1 6 (1234); (1243); (1324); (1342); (1423); (1432)
 
 

Untergruppen

Nach dem Satz von Lagrange sind nur Untergruppen mit den folgenden Ordnungen möglich: 2; 3; 4; 6; 8 und 12.

A4

Die bis auf Isomorphie bestimmte 12-elementige Untergruppe haben wir schnell gefunden; dabei muss es sich um die alternierende Gruppe A4\bm{A_4} handeln. Diese enthält alle Permutationen aus der obigen Tabelle mit dem Signum +1 und wird z.B. von (12)(34) und (123) erzeugt.

Zyklische Gruppen

Es treten in der S4\bm{S_4} nichttriviale Elemente mit den Ordnungen 2; 3 und 4 auf. Diese erzeugen die entsprechenden zyklischen Gruppen C2\bm{C_2} (9 mal), C3\bm{C_3} (4 mal) und C4\bm{C_4} (3 mal). Dabei enthalten die C4\bm{C_4} isomorphen Gruppen neben zwei Permutationen der Ordnung 4 auch jeweils eine gerade Permutation der Ordnung 2.

Symmetrische Gruppe

Die symmetrische Gruppe S3\bm{S_3} ist vierfach in der S4\bm{S_4} enthalten. Die Untergruppen werden jeweils von einer ungeraden Permutation der Ordnung 2 und einer Permutation der Ordnung 3 erzeugt. Diese Untergruppen sind weiterhin dadurch charakterisiert, dass sie genau ein Element festlassen, es also gemäß Satz 5210D genau die Permutationen mit einelementigen Fixmengen sind.

Diedergruppen

Die Diedergruppe D3\bm{D_3} ist als S3\bm{S_3} Untergruppe der S4\bm{S_4}. Die beiden anderen nichttrivialen Diedergruppen D2\bm{D_2} und D4\bm{D_4} sind ebenso Untergruppen.
Damit ist die Untergruppenstruktur der symmetrischen Gruppe S4\bm{S_4} vollständig aufgeklärt. Die folgende Grafik veranschaulicht den Zusammenhang der Untergruppentypen.
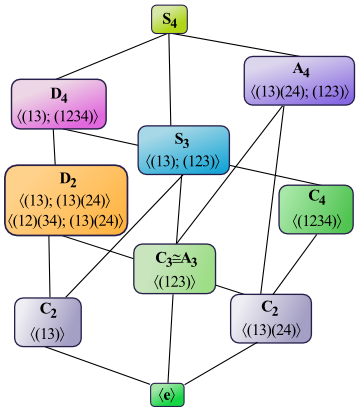
S4Ugs.png
Untergruppentypen der S4\bm{S_4}

Vorkommen

Die S4\bm S_4 ist die Symmetriegruppe eines regulären Tetraeders.

Ich stimme mit der Mathematik nicht überein. Ich meine, daß die Summe von Nullen eine gefährliche Zahl ist.

Stanislaw Jerzy Lec

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Spezielle Gruppen