Symmetrische Gruppe S3
Die symmetrische Gruppe besteht aus 6 Elementen, den Permutationen einer dreielementigen Menge. In Zyklenschreibweise ergibt sich folgende Gruppentafel.
| (1) | (123) | (132) | (12) | (13) | (23) |
| (123) | (132) | (1) | (13) | (23) | (12) |
| (132) | (1) | (123) | (23) | (12) | (13) |
| (12) | (23) | (13) | (1) | (132) | (123) |
| (13) | (12) | (23) | (123) | (1) | (132) |
| (23) | (13) | (12) | (132) | (123) | (1) |
Auch die Untergruppen der lassen sich relativ einfach aufklären.
Einerseits gibt es eine zur isomorphe Untergruppe, die von der Permutation (123) erzeugt wird. Diese Untergruppe ist auch genau die alternierende Gruppe .
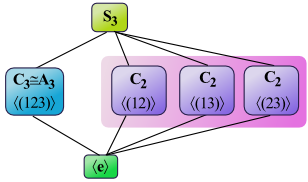
Untergruppengraph der
Der Zusammenhang zwischen den einzelnen Untergruppen wird durch den Untergruppengraphen veranschaulicht.
Die ganzen Zahlen hat der liebe Gott geschaffen, alles andere ist Menschenwerk.
Leopold Kronecker
Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf
ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld
• Dοrfplatz 25 • 17237 Blankеnsее
• Tel.: 01734332309 (Vodafone/D2) •
Email: cο@maτhepedιa.dе