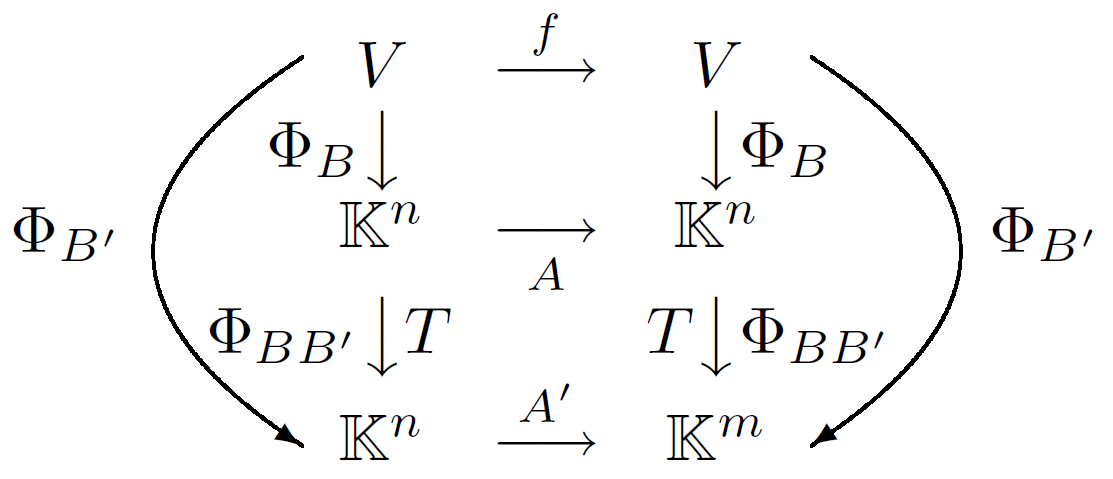Ähnlichkeit von Matrizen, Problem der Diagonalisierbarkeit

Bw.png
Bei Endomorphismen f ⁣:V→Vf\colon V \to V (mit n=dim⁡V<∞n = \dim V < \infty) betrachten wir Darstellungsmatrizen AA bezüglich derselben Basis B={b1,…,bn}B = \{ b_1,\dots,b_n \} in Urbildraum gleich Bildraum VV.
Bei einem Basiswechsel B→B′B \to B' mit zugehörigen Koordinaten-Transformationen ξ′=T⋅ξ\xi' = T \cdot \xi gilt für die Darstellungsmatrizen A′=T⋅A⋅T −1A' = T \cdot A \cdot T^{\, -1} mit einer regulären Matrix TT (siehe Folgerung 816E).

Definition

Zwei quadratische Matrizen A,A′∈Mat(n×n,K)A,A' \in \Mat(n\cross n,{\mathbb{K}}) heißen ähnlich, in Zeichen A≈A′A \approx A', wenn eine reguläre Matrix T∈Mat(n×n,K)T \in \Mat(n\cross n,{\mathbb{K}}) existiert mit A′=TAT−1A' = T A T^{-1}.

Bemerkung

  1. Dies ist wieder eine mengentheoretische Äquivalenzrelation in Mat(n×n,K)\Mat(n\cross n,{\mathbb{K}}). Ähnliche Matrizen sind auch äquivalent, A≈A′⇒A∼A′A \approx A' \Rightarrow A \sim A', aber die Äquivalenzklassen bezüglich ∼\sim werden durch die Ähnlichkeitsklassen weiter aufgegliedert.
  2. Ähnliche Matrizen können aufgefasst werden als Darstellungsmatrizen derselben linearen Abbildung ff bei nur anders gewählten (aber in Urbild- und Bildraum gleichen) Basen.
Problem: Wir suchen wieder einfache Repräsentanten in den Ähnlichkeitsklassen, das heißt Normalformen ähnlicher Matrizen. Eine Normalform Dr=(1⋱1⋱0)D_r = \begin{pmatrix} 1 \\ && \ddots \\ & && 1 \\ & && & \ddots \\ &&&&& 0 \end{pmatrix} wie bei den äquivalenten Matrizen ist im allgemeinen nicht zu erreichen. Weitere einfache Kandidaten für solche Normalformen sind Diagonalmatrizen D=diag⁡(λ1,…,λn)=(λ10⋱0λn)D = \diag(\lambda_1,\dots,\lambda_n) = \begin{pmatrix} \lambda_1 & & 0 \\ & \ddots \\ 0 & & \lambda_n \end{pmatrix}. Vorläufiges Normalformenproblem: Welche Matrizen sind einer Diagonalmatrix ähnlich?

Diagonalisierbarkeit

Ein Endomorphismus f ⁣:V→Vf \colon V \to V (dim⁡V=n<∞\dim V = n < \infty) heißt diagonalisierbar, wenn er eine Diagonalmatrix D=diag⁡(λ1,…,λn)D = \diag(\lambda_1,\dots,\lambda_n) als Darstellungsmatrix bezüglich einer Basis B={b1,…,bn}B = \{ b_1,\dots,b_n \} besitzt. Eine Matrix A∈M(n,n,K)A \in M(n,n,{\mathbb{K}}) diagonalisierbar, wenn sie ähnlich zu einer Diagonalmatrix ist.

Beispiel

Es gilt (1002)≈(1102)\left(\begin{array}{c} 1&0\\0&2\end{array}\right)\approx\left(\begin{array}{c}1&1\\0&2\end{array}\right), denn für S=(1101)S=\left(\begin{array}{c}1&1\\0&1 \end{array}\right) gilt S−1=(1−101)S^{-1}=\left(\begin{array}{c}1&-1\\0&1 \end{array}\right) und S−1⋅(1102)⋅S S^{-1}\cdot\left(\begin{array}{c}11 \\ 02\end{array}\right)\cdot S =(1−101)⋅(1102)⋅(1101) =\left(\begin{array}{c}1&-1\\0&1 \end{array}\right)\cdot\left(\begin{array}{c}11 \\ 02\end{array}\right)\cdot \left(\begin{array}{c}1&1\\0&1 \end{array}\right) =(1−101)⋅(1202)=\left(\begin{array}{c}1&-1\\0&1 \end{array}\right)\cdot\left(\begin{array}{c}1&2\\0&2 \end{array}\right) =(1002)=\left(\begin{array}{c} 1&0\\0&2\end{array}\right)
(1102)\left(\begin{array}{c} 1&1\\0&2\end{array}\right) ist also diagonalisierbar.

Bemerkung

Ähnliche Matrizen haben die gleichen Eigenwerte, aber nicht die gleichen Eigenvektoren. Ist beispielsweise Av=λvAv=\lambda v und B=S−1ASB=S^{-1}AS, so gilt für w=S−1vw=S^{-1}v Bw=S−1ASS−1v Bw=S^{-1}ASS^{-1}v =S−1Av =S^{-1}Av =S−1λv =S^{-1}\lambda v =λS−1v =\lambda S^{-1}v =λw, =\lambda w, aber meistens w≠vw\neq v.
(1002)\left(\begin{array}{c}1&0\\0&2\end{array}\right) hat Eigenwerte 1,21, 2 und Eigenvektoren (10)\left(\begin{array}{c}1\\0\end{array}\right), (01)\left(\begin{array}{c}0\\1\end{array}\right). (1102)\left(\begin{array}{c}1&1\\0&2\end{array}\right) hat Eigenwerte 1,21, 2 und Eigenvektoren (10)\left(\begin{array}{c}1\\0 \end{array}\right), (11)\left(\begin{array}{c}1\\1 \end{array}\right).

Satz 817H (Diagonalisierbarkeit und Eigenvektoren)

f ⁣:V→Vf \colon V \to V (dim⁡V=n<∞\dim V = n < \infty) ist diagonalisierbar    ⟺   \,\iff\, Es existiert eine Basis B={b1,…,bn}B = \{ b_1,\dots,b_n \} von VV aus Eigenvektoren mit der Eigenschaft ∀k=1n f(bk)=λkbk\forall_{k=1}^n\, f(b_k) = \lambda_kb_k mit λk∈K\lambda_k \in K.

Beweis

Sind λ1,…,λn\lambda_1,\dots,\lambda_n gerade die Eigenwerte von ff so ist diag⁡(λ1,…,λn)\diag(\lambda_1,\dots,\lambda_n) genau die Darstellungsmatrix für eine Basis bestehend aus Eigenvektoren. □\qed
Aus Satz 817H und Satz 816J ergibt sich:

Folgerung 817I

Ein Endomorphismus f ⁣:V→Vf \colon V \to V mit dim⁡V=n<∞\dim V = n < \infty ist diagonalisierbar   ⟺  \iff V=Eλ1⊕⋯⊕EλmV = E_{\lambda_1} \oplus \dots \oplus E_{\lambda_m} mit paarweise verschiedenen Eigenwerten λ1,…,λm\lambda_1,\dots,\lambda_m   ⟺  \iff n=d1+⋯+dmn = d_1 + \dots + d_m mit den zugehörigen geometrischen Vielfachheiten d1,…,dmd_1,\dots,d_m.

Bemerkung

Im allgemeinen kann man nur zeigen: V=Eλ1⊕⋯⊕Eλm⊕UV = E_{\lambda_1} \oplus \dots \oplus E_{\lambda_m} \oplus U mit einem "Rest"-Unterraum UU, der keine Eigenvektoren mehr enthält, mit der Dimension n−∑i=1mdi≥0n - \sum\limits_{i=1}^m d_i \ge 0 (Schlimmster Fall: V=UV = U). Zur Lösung des allgemeinen Normalformenproblems für ähnliche Matrizen muss dieser Restraum weiter untersucht werden.

Satz 81FG

  1. Sei f∈EndK(V)f\in\End_K(V) ein Endomorphismus und A,B{A},{B} Basen von VV. Dann sind die Darstellungsmatrizen von ff bezüglich AA und BB ähnlich: MAA(f)∼MBB(f)M^{\cal A}_{\cal A}(f)\sim M^{\cal B}_{\cal B}(f) .
  2. Sei A∈Mat(n×n,K)A\in\Mat(n\times n, K) eine quadratische Matrix und f:Kn⟶Knf:K^n \longrightarrow K^n die zugehörige lineare Abbildung (A=MEE(f)\nohtml A=M^{E}_{E}(f) für eine Basis EE ). Dann ist AA genau dann diagonalisierbar, wenn ff diagonalisierbar ist.

Beweis

(i): Es gilt (Satz 16B1): MBA(id⁡)⋅MAA(f)⋅MAB(id⁡)=MBB(f), M^{\cal A}_{\cal B}(\id)\cdot M^{\cal A}_{\cal A}(f)\cdot M^{\cal B}_{\cal A}(\id)=M_{\cal B}^{\cal B}(f), also MBB(f)=S−1⋅MAA(f)⋅S M_{\cal B}^{\cal B}(f)=S^{-1}\cdot M^{\cal A}_{\cal A}(f)\cdot S mit S=MAB(id⁡)S=M^{\cal B}_{\cal A}(\id). (ii) "⇒\Rightarrow": Sei AA diagonalisierbar ⇒∃S \Rightarrow\exists S mit S−1AS=D S^{-1}AS=D und DD diagonal. Nun ist MSE(id⁡)=S−1M^{\cal E}_S(\id)=S^{-1}, wenn man die Spalten von SS als Basis von VV auffasst. Dies ist möglich, da SS invertierbar ist. Damit gilt D=S−1AS D=S^{-1}AS =MSE(id⁡)⋅MEE(f)⋅MES(id⁡) =M^{\cal E}_S(\id)\cdot M_{\cal E}^{\cal E}(f)\cdot M^S_{\cal E}(\id) =MSS(f) =M^S_S(f) . Also ist ff diagonalisierbar. "⇐\Leftarrow": Sei ff diagonalisierbar. Dann gibt es eine Basis B{\cal B} mit MBB(f)=DM^{\cal B}_{\cal B}(f)=D. Da MEE(f)=AM^{\cal E}_{\cal E}(f)=A folgt die Behauptung aus (i). Also A≈DA\approx D. □\qed

Bemerkung

Nach Satz 81FG können wir uns also bei Betrachtungen zur Diagonalisierbarkeit (von Endomorphismen) immer auf die Diagonalisierbarkeit von Matrizen zurückziehen. Wenn wir f∈EndK(V)f\in\End_K(V) diagonalisieren möchten, wählen wir eine beliebige Basis A{\cal A} von VV und diagonalisieren MAA(f)M^{\cal A}_{\cal A}(f) als Matrix.
 
 

Es ist unmöglich, die Schönheiten der Naturgesetze angemessen zu vermitteln, wenn jemand die Mathematik nicht versteht. Ich bedaure das, aber es ist wohl so.

Richard Feynman

Copyright Missing!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Lineare Algebra