Wachstum bei beschränkten Ressourcen

Wir wollen mittels einer Differentialgleichung das Wachstum einer Population modellieren.

Sei $x(t)$ die Anzahl der Individuen zum Zeitpunkt $t$. Mit $a$ bezeichnen wir die vorhandenen Nahrungsmittel pro Zeiteinheit und mit $b$ den Durchschnittsverbrauch der Lebewesen.

Der Term $a-bx(t)$ beschreibt dann gerade die überschüssige Nahrungsmittelmenge.

Die Wachstumsrate der Population kann durch die erste Ableitung $x'(t)$ ausgedrückt werden. Diese soll in unserem Modell gerade von der Anzahl der Individuen und der überschüssigen Nahrungsmittelmenge abhängen. Die DGL lautet damit:

oder kürzer $x'=x(a-bx)$. Dabei handelt es sich um eine DGL mit getrennten Variablen:

Für den Ausdruck auf der linken Seite führen wir eine Partialbruchzerlegung mit dem Ansatz

durch, was auf $1=Pa-Pbx+Qx$ führt. Der Koeffizientenvergleich liefert das Gleichungssystem:

$1=Pa$ und $Pb+Q=0$ $\implies P=\dfrac 1 a$; $Q=\dfrac b a$.

Zum Zeitpunkt $t=0$ soll eine Anfangspopulation von $x_0$ Individuen vorhanden sein. Das Integral (1) wird damit zum Anfangswertproblem

mit der Lösung $\ntxbraceIC{\dfrac 1 a\ln|x| - \dfrac 1 a \ln|a-bx|}_{x_0}^x$ $=\ntxbraceIC{\dfrac 1 a \ln\ntxbraceI{ \dfrac x {a-bx}}}_{x_0}^x =t$.

$\implies \dfrac 1 a \ln\ntxbraceI{ \dfrac x {a-bx}}-\dfrac 1 a \ln\ntxbraceI{ \dfrac {x_0} {a-bx_0}}=t$ $\implies \dfrac 1 a \ln\ntxbraceI{ \dfrac x {a-bx}}=t+\dfrac 1 a \ln\ntxbraceI{ \dfrac {x_0} {a-bx_0}}$ $\implies \ln\ntxbraceI{ \dfrac x {a-bx}}=at+\ln\ntxbraceI{ \dfrac {x_0} {a-bx_0}}$

$\implies \dfrac x {a-bx}= \dfrac {x_0} {a-bx_0}\e^{at}$ $\implies xa-xbx_0=ax_0 \e^{at}-bxx_0\e^{at}$ $\implies xa-xbx_0+bxx_0\e^{at}=ax_0 \e^{at}$ $\implies x(a-bx_0+bx_0\e^{at})=ax_0 \e^{at}$

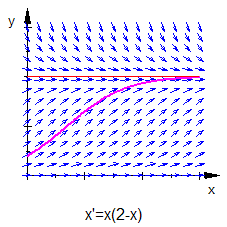
Bildet man den Grenzwert für $t\to\infty$ so ergibt sich $x\to\dfrac a b$. Das System strebt also langfristig einen stabilen Zustand an, und es gilt für große $t$: $a-bx\approx 0$, was nichts anderes bedeutet, als das die vorhandenen Nahrungsmittel ausgeschöpft werden.

Das Vektorfeld der DLG in der Grafik veranschaulicht außerdem, dass für Startwerte $x_0$, die sehr viel größer als $\dfrac a b$ sind, die Anzahl der Individuum sehr schnell abnimmt. Das Futter reicht nicht, und es muss erst einmal heftig gestorben werden, bis der Gleichgewichtszustand erreicht ist.