Exakte Differentialgleichungen

Eine Differentialgleichung der Form
p(x,y)+y′q(x,y)=0p(x,y)+y'q(x,y)=0
heißt exakte Differentialgleichung, wenn es eine Funktion F(x,y)F(x,y) gibt, so dass p(x,y)=∂F(x,y)∂xp(x,y)=\dfrac {\partial F(x,y)} {\partial x} und q(x,y)=∂F(x,y)∂yq(x,y)=\dfrac {\partial F(x,y)} {\partial y}.
Bei einer so gegebenen exakten DGL ist die Lösung in impliziter Form sofort klar: F(x,y)=CF(x,y)=C.
Benutzen wir die verallgemeinerte Kettenregel, so gilt ∂F(x,y)∂x+∂F(x,y)∂yy′=0\dfrac {\partial F(x,y)} {\partial x}+\dfrac {\partial F(x,y)} {\partial y}y'=0; setzen wir hier pp und qq ein, so ist die DGL erfüllt.

Beispiele

Beispiel 1

4x3y+(y2+x4)y′=04x^3y+(y^2+x^4)y'=0
F(x,y)=yx4+13y3F(x,y)=yx^4+\dfrac 1 3 y^3 ∂F(x,y)∂x=4x3y\dfrac {\partial F(x,y)} {\partial x}=4x^3y und ∂F(x,y)∂y=y2+x4\dfrac {\partial F(x,y)} {\partial y}=y^2+x^4
Lösung: yx4+13y3=Cyx^4+\dfrac 1 3 y^3=C

Beispiel 2

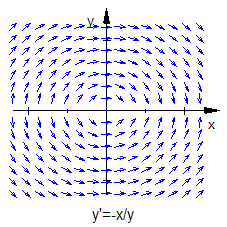
271_Kreis.png
y′=−xyy'=-\dfrac x y (vgl. Beispiel 166V) x+yy′=0x+yy'=0
F(x,y)=12x2+12y2F(x,y)=\dfrac 1 2 x^2 +\dfrac 1 2 y^2
Lösung: x2+y2=2Cx^2+y^2=2C

Bemerkung

Wissen wir, dass eine DGL exakt ist, so können wir sie folgendermaßen lösen: Wir integrieren zuerst pp nach xx und ermitteln die verbleibende Konstante C(y)C(y) aus der Gleichung ∂F(x,y)∂y=q\dfrac {\partial F(x,y)} {\partial y}=q (oder umgekehrt). Satz 167V liefert das nötige Kriterium um eine DGL auf Exaktheit zu testen.

Beispiel

y+(x+2y)y′=0y+\braceNT{x+\dfrac 2 y}y'=0 ist eine exakte Differentialgleichung.
Es ist ∂F∂x=y\dfrac {\partial F} {\partial x}=y. Daher ist F(x,y)=∫yd⁡xF(x,y)=\int\limits y\d x =xy+C(y)=xy+C(y)
∂F∂y=x+C′(y)\dfrac {\partial F} {\partial y}=x+C'(y) =x+2y=x+\dfrac 2 y   ⟹  C′(y)=2y\implies C'(y)=\dfrac 2 y   ⟹  \implies C(y)=2ln⁡yC(y)=2\ln y.
F(x,y)=xy+2ln⁡yF(x,y)=xy+2\ln y
 
 

Hochtechnologie ist im wesentlichen mathematische Technologie.

Enquete-Kommission der Amerikanischen Akademie der Wissenschaften

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Gewöhnliche Differentialgleichungen