Differentialgleichungen mit getrennten Variablen

Eine Differentialgleichung mit getrennten Variablen hat die Gestalt
y´=g(x)⋅h(y)y´=g(x)\cdot h(y),(1)
die rechte Seite lässt sich also in Produktform schreiben, wobei der eine Faktor nur von xx und der andere nur von yy abhängt.
Zur Lösung formt man (1) in y´h(y)=g(x)\dfrac {y´} {h(y)}=g(x) um und findet die Lösung durch Integration beider Seiten:
∫d⁡yh(y)=∫g(x)d⁡x\int\limits\dfrac {\d y} {h(y)}=\int\limits g(x)\d x
Wenn möglich, löst man das Ergebnis dann nach yy auf, andernfalls erhält man eine implizite Funktion.
Liegt eine Differentialgleichung nicht in Form (1) vor, so kann es dennoch möglich sein, sie in diese Form zu überführen. Dann spricht man von der Trennung der Variablen oder Trennung der Veränderlichen.

Beispiele

Beispiel 166V

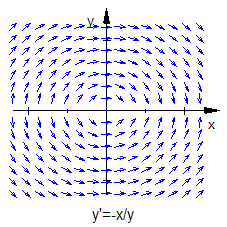
271_Kreis.png
y´=−xyy´=-\dfrac x y (2)
  ⟹  \implies y′y=−xy'y=-x   ⟹  \implies ∫yd⁡y=−∫xd⁡x\int\limits y\d y=-\int\limits x\d x   ⟹  \implies y22=−x22+C\dfrac {y^2} 2=-\dfrac {x^2} 2 + C
  ⟹  \implies x2+y2=2Cx^2+y^2=2C.
Dies ist eine Kreisgleichung (Formel 15VR). Bei der Lösungsmenge handelt es sich also um konzentrische Kreise um den Ursprung. Dieses Beispiel zeigt auch, dass es nicht immer sinnvoll ist, nach einer expliziten Form der Lösung zu suchen, da uns dann eine Kreishälfte verloren ginge.
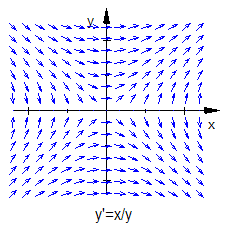
272_Hyperbeln.png
Ändern wir in der Differentialgleichung (2) das Vorzeichen: y´=xyy´=\dfrac x y, so können wir den Rechenweg unter Beachtung des geänderten Vorzeichens übernehmen und erhalten als Lösung Kurven der Gestalt y2−x2=2Cy^2-x^2=2C, wobei es sich um Hyperbeln handelt.
 
 

Wie ist es möglich, daß die Mathematik, letztlich doch ein Produkt menschlichen Denkens unabhängig von der Erfahrung, den wirklichen Gegebenheiten so wunderbar entspricht?

Albert Einstein

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Gewöhnliche Differentialgleichungen