Lineare Differentialgleichungen erster Ordnung

Eine lineare Differentialgleichung erster Ordnung hat die Form
y′+g(x)y=h(x)y'+g(x)y=h(x)
Dabei sollen g,hg,h stetig differenzierbare Funktionen sein.
Gleichungen dieser Gestalt werden in zwei Schritten gelöst:

Homogene Differentialgleichung

Ist die rechte Seite 0, so spricht man von einer homogenen linearen Differentialgleichung.
y′+g(x)y=0y'+g(x)y=0
Die Nullfunktion y≡0y\equiv 0 ist stets triviale Lösung dieser Gleichung.
Die nichttrivialen Lösungen der DGL können durch Trennung der Variablen gefunden werden.
∫d⁡yy=−∫g(x)d⁡x\int\limits \dfrac {\d y} y=-\int\limits g(x) \d x   ⟹  ln⁡∣y∣=−∫g(x)d⁡x+C1\implies \ln|y|=-\int\limits g(x) \d x+C_1   ⟹  ∣y∣=C2e⁡−∫g(x)d⁡x\implies |y|=C_2\e ^{-\int\limits g(x) \d x} (C2>0C_2>0)
y=Ce⁡−∫g(x)d⁡xy=C\e ^{-\int\limits g(x) \d x} C∈RC\in\R beliebig (1)

Beispiel

y′+yx=0y'+\dfrac {y} {x} =0 Die Lösungsformel ergibt: y=Ce⁡−∫d⁡xxy=C\e^{-\int\limits \dfrac {\d x} {x}} =Ce⁡−ln⁡(x)=C\e^{-\ln (x)} =Cx=\dfrac C {x}

Inhomogene Differentialgleichung

Da hierbei angewendete Verfahren heißt Variation der Konstanten. Dabei wird die Integrationskonstante aus Formel (1) als Variable C(x)C(x) angesehen. Bezeichnen wir die spezielle Lösung der homogenen Gleichung mit yh:=e⁡−∫g(x)d⁡xy_h:=\e ^{-\int\limits g(x) \d x}, so gilt: y=C(x)e⁡−∫g(x)d⁡xy=C(x)\e ^{-\int\limits g(x) \d x} =C(x)yh=C(x)y_h.
y′=C′(x)yh+C(x)yh′y'=C'(x)y_h+C(x)y_h'
y′+g(x)y=h(x)y'+g(x)y=h(x)   ⟹  \implies C′(x)yh+C(x)yh′+g(x)C(x)yh=h(x)C'(x)y_h+C(x)y_h'+g(x)C(x)y_h=h(x)   ⟹  \implies C′(x)yh+C(x)(yh′+g(x)yh)=h(x)C'(x)y_h+C(x)(y_h'+g(x)y_h)=h(x)
Da yhy_h Lösung der homogenen DGL (yh′+g(x)yh=0y_h'+g(x)y_h=0): C′(x)yh=h(x)C'(x)y_h=h(x)   ⟹  C′(x)=h(x)yh\implies C'(x)=\dfrac {h(x)} {y_h}   ⟹  C(x)=∫h(x)yhd⁡x+D\implies C(x)=\int\limits \dfrac {h(x)} {y_h}\d x+D
Die Lösung der inhomogenen Gleichung:
y=yh(∫h(x)yhd⁡x+D)y=y_h\braceNT{\int\limits \dfrac {h(x)} {y_h}\d x+D}

Beispiel 168L

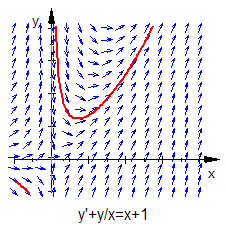
282_Bsp.png
y′+yx=x+1y'+\dfrac {y} {x} =x+1. Die spezielle Lösung der homogenen Gleichung war yh=1xy_h=\dfrac 1 x.
y=1x(∫(x+1)xd⁡x+D)y=\dfrac 1 x\braceNT{\int\limits(x+1) x \d x+D} =1x(∫(x2+x)d⁡x+D)=\dfrac 1 x\braceNT{\int\limits (x^2+ x) \d x+D} =1x(x33+x22+D)=\dfrac 1 x\braceNT{\dfrac{x^3} 3+ \dfrac {x^2} 2+D} =x23+x2+Dx=\dfrac{x^2} 3+ \dfrac {x} 2+\dfrac D x
 
 

Es gibt jedoch noch einen anderen Grund für die hohe Wertschätzung der Mathematik; sie allein bietet den Naturwissenschaften ein gewisses Maß an Sicherheit, das ohne Mathematik nicht erreichbar wäre.

Albert Einstein

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Gewöhnliche Differentialgleichungen