Beispiele

Wir wollen die Lösung der Differentialgleichung

y'=-\dfrac {1+y^2}{xy}

mit der Anfangsbedingung

y(1)=2

ermitteln.

Die Trennung der Variablen lässt sich leicht herbeiführen:

\int\limits \dfrac y {1+y^2}\d y=\int\limits -\dfrac 1 x\d x

\implies\dfrac 1 2 \ln(1+y^2)=-\ln x+C

\implies 1+y^2=\e^{-2\ln x+2C}

=\e^{-2\ln x}\cdot\e^{2C}

\implies 1+y^2=\dfrac K {x^2}

(mit

K=\e^{2C}

K>0

)

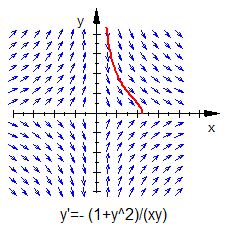
Durch Einsetzen finden wir für das Anfangswertproblem die Lösung

K=5

und damit ergibt sich

y=\sqrt{\dfrac 5 {x^2} -1}

Der negative Zweig der Wurzelfunktion kommt dabei nicht in Frage, da

y(1)=2>0

gelten muss.

Im großen Garten der Geometrie kann sich jeder nach seinem Geschmack einen Strauß pflücken.

David Hilbert

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.

Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld • Dοrfplatz 25 • 17237 Blankеnsее • Tel.: 01734332309 (Vodafone/D2) • Email: cο@maτhepedιa.dе