Der schwimmende Hund
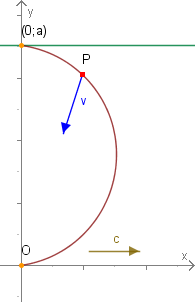
Ein Hund ist fatalerweise ans falsche Flussufer gekommen (
Punkt (0;a)) und möchte gerne zu seinem Herrchen, der sich im Nullpunkt langweilt, zurück schwimmen. Der Hund schwimme mit der Geschwindigkeit
v v v und der Fluss habe die Strömungsgeschwindigkeit
c c c .
Da der Hund ein etwas dümmliches Tier ist, schwimmt er immer genau auf sein Herrchen zu.
Mit gesunden Menschenverstand vermuten wir nun, dass für
v > c v>c v > c der Hund beim Herrchen ankommt, für
c > v c>v c > v jedoch abgetrieben wird. Was passiert im Fall
v = c v=c v = c ? Auf welcher Kurve schwimmt der Hund?
Aufstellen der DGL
Die Position des Hundes zur Zeit
t t t sei
P ( t ) = ( x ( t ) , y ( t ) ) P(t)=(x(t),y(t)) P ( t ) = ( x ( t ) , y ( t ) ) . Da der Hund immer genau auf sein Herrchen zuschwimmt, ist sein Geschwindigkeitsvektor
v ⋅ − ( x ( t ) , y ( t ) ) ∣ ∣ ( x ( t ) , y ( t ) ) ∣ ∣ v\cdot \dfrac{-(x(t),y(t))}{||(x(t),y(t))||} v ⋅ ∣ ∣ ( x ( t ) , y ( t ) ) ∣ ∣ − ( x ( t ) , y ( t ) ) = v ⋅ − ( x ( t ) , y ( t ) ) x 2 ( t ) + y 2 ( t ) =v\cdot \dfrac{-(x(t),y(t))}{\sqrt{x^2(t)+y^2(t)}} = v ⋅ x 2 ( t ) + y 2 ( t ) − ( x ( t ) , y ( t ) ) Die Gesamtgeschwindigkeit
( x ˙ ( t ) , y ˙ ( t ) ) (\dot x(t),\dot y(t)) ( x ˙ ( t ) , y ˙ ( t ) ) ergibt sich aus den Summen der Hundegeschwindigkeit und der Strömungsgeschwindigkeit des Flusses.
( x ˙ ( t ) , y ˙ ( t ) ) = v ⋅ − ( x ( t ) , y ( t ) ) x 2 ( t ) + y 2 ( t ) + ( c , 0 ) (\dot x(t),\dot y(t))=v\cdot \dfrac{-(x(t),y(t))}{\sqrt{x^2(t)+y^2(t)}}+(c,0) ( x ˙ ( t ) , y ˙ ( t ) ) = v ⋅ x 2 ( t ) + y 2 ( t ) − ( x ( t ) , y ( t ) ) + ( c , 0 ) x ˙ ( t ) = − v x 2 ( t ) + y 2 ( t ) x ( t ) + c \dot x(t)=\dfrac {-v} {\sqrt{x^2(t)+y^2(t)}} x(t)+c x ˙ ( t ) = x 2 ( t ) + y 2 ( t ) − v x ( t ) + c y ˙ ( t ) = − v x 2 ( t ) + y 2 ( t ) y ( t ) \dot y(t)=\dfrac {-v} {\sqrt{x^2(t)+y^2(t)}} y(t) y ˙ ( t ) = x 2 ( t ) + y 2 ( t ) − v y ( t ) Es gilt
y ′ = d y d x = d y d t ⋅ d t d x = y ˙ x ˙ y'=\dfrac {\d y}{\d x}=\ \dfrac {\d y}{\d t}\cdot \dfrac {\d t} {\d x}=\dfrac {\dot y} {\dot x} y ′ = d x d y = d t d y ⋅ d x d t = x ˙ y ˙ (vgl.
Tangentialvektor einer ebenen Kurve ).
y ′ = − v y x 2 + y 2 − v x x 2 + y 2 + c y'=\dfrac {\dfrac {-vy} {\sqrt{x^2+y^2}} } {\dfrac {-vx} {\sqrt{x^2+y^2}} +c} y ′ = x 2 + y 2 − v x + c x 2 + y 2 − v y = − v y − v x + c x 2 + y 2 =\dfrac {-vy} {-vx+c\sqrt{x^2+y^2}} = − v x + c x 2 + y 2 − v y = v y v x − c x 2 + y 2 =\dfrac {vy} {vx-c\sqrt{x^2+y^2}} = v x − c x 2 + y 2 v y = v y x v − c 1 + ( y x ) 2 =\dfrac {v\dfrac y x} {v-c\sqrt{1+\braceNT{ \dfrac y x}^2}} = v − c 1 + ( x y ) 2 v x y Lösen der DGL
f ( z ) − z = v z v − c 1 + z 2 − z f(z)-z=\dfrac{vz}{v-c\sqrt{1+z^2}}-z f ( z ) − z = v − c 1 + z 2 v z − z = v z − v z + c z 1 + z 2 v − c 1 + z 2 =\dfrac {vz -vz+cz\sqrt{1+z^2}}{v-c\sqrt{1+z^2}} = v − c 1 + z 2 v z − v z + c z 1 + z 2 = c z 1 + z 2 v − c 1 + z 2 =\dfrac {cz\sqrt{1+z^2}}{v-c\sqrt{1+z^2}} = v − c 1 + z 2 c z 1 + z 2 d z f ( z ) − z = v − c 1 + z 2 c z 1 + z 2 d z \dfrac {\d z}{f(z)-z}=\dfrac{v-c\sqrt{1+z^2}} {cz\sqrt{1+z^2}}\d z f ( z ) − z d z = c z 1 + z 2 v − c 1 + z 2 d z = ( v c ⋅ 1 z 1 + z 2 − 1 z ) d z =\braceNT {\dfrac v c\cdot \dfrac{1} {z\sqrt{1+z^2}}-\dfrac 1 z}\d z = ( c v ⋅ z 1 + z 2 1 − z 1 ) d z = d x x =\dfrac {\d x} x = x d x ∫ ( v c ⋅ 1 z 1 + z 2 − 1 z ) d z \int\limits \braceNT {\dfrac v c\cdot \dfrac{1} {z\sqrt{1+z^2}}-\dfrac 1 z}\d z ∫ ( c v ⋅ z 1 + z 2 1 − z 1 ) d z = ∫ d x x =\int\limits \dfrac {\d x} x = ∫ x d x v c ⋅ ∫ 1 z 1 + z 2 d z − ∫ 1 z d z \dfrac v c\cdot \int\limits \dfrac{1} {z\sqrt{1+z^2}}\d z- \int\limits\dfrac 1 z\d z c v ⋅ ∫ z 1 + z 2 1 d z − ∫ z 1 d z = ∫ d x x =\int\limits \dfrac {\d x} x = ∫ x d x − v c ln 1 + 1 + z 2 z − ln z = ln x + C -\dfrac v c\ln\dfrac {1+\sqrt{1+z^2}} z -\ln z=\ln x+C − c v ln z 1 + 1 + z 2 − ln z = ln x + C (
Beispiel 167I )
Rücksubstitution:
− v c ln x + x 2 + y 2 y − ln y x = ln x + C -\dfrac v c\ln\dfrac {x+\sqrt{x^2+y^2}} y -\ln \dfrac y x=\ln x+C − c v ln y x + x 2 + y 2 − ln x y = ln x + C ⟹ − v c ln x + x 2 + y 2 y − ln y + ln x = ln x + C \implies -\dfrac v c\ln\dfrac {x+\sqrt{x^2+y^2}} y -\ln y +\ln x=\ln x+C ⟹ − c v ln y x + x 2 + y 2 − ln y + ln x = ln x + C ⟹ − v c ln x + x 2 + y 2 y = ln y + C \implies -\dfrac v c\ln\dfrac {x+\sqrt{x^2+y^2}} y=\ln y+C ⟹ − c v ln y x + x 2 + y 2 = ln y + C ⟹ − v ln x + x 2 + y 2 y = c ln y + C 1 \implies -v \ln\dfrac {x+\sqrt{x^2+y^2}} y=c\ln y+C_1 ⟹ − v ln y x + x 2 + y 2 = c ln y + C 1 ⟹ − v ln ( x + x 2 + y 2 ) + v ln y = c ln y + C 1 \implies -v \ln (x+\sqrt{x^2+y^2}) +v\ln y=c\ln y+C_1 ⟹ − v ln ( x + x 2 + y 2 ) + v ln y = c ln y + C 1 ⟹ − v ln ( x + x 2 + y 2 ) = ( c − v ) ln y + C 1 \implies -v \ln (x+\sqrt{x^2+y^2})=(c-v)\ln y+C_1 ⟹ − v ln ( x + x 2 + y 2 ) = ( c − v ) ln y + C 1 ⟹ v ln ( x + x 2 + y 2 ) = ( v − c ) ln y + C 2 \implies v \ln (x+\sqrt{x^2+y^2})=(v-c)\ln y+C_2 ⟹ v ln ( x + x 2 + y 2 ) = ( v − c ) ln y + C 2 ⟹ ln ( x + x 2 + y 2 ) = ( 1 − c v ) ln y + C 3 \implies \ln (x+\sqrt{x^2+y^2})=(1-\dfrac c v)\ln y+C_3 ⟹ ln ( x + x 2 + y 2 ) = ( 1 − v c ) ln y + C 3 Lösung in impliziter Form:
x + x 2 + y 2 = K y 1 − c v x+\sqrt{x^2+y^2}=Ky^{1- \dfrac c v} x + x 2 + y 2 = K y 1 − v c Einsetzen des Anfangswerts
( x , y ) = ( 0 , a ) (x,y)=(0,a) ( x , y ) = ( 0 , a ) ergibt:
a = K a 1 − c v a=Ka^{1- \frac c v} a = K a 1 − v c ⟹ K = a c v \implies K=a^{\frac c v} ⟹ K = a v c .
x + x 2 + y 2 = a c v y 1 − c v x+\sqrt{x^2+y^2}=a^{\frac c v}y^{1- \frac c v} x + x 2 + y 2 = a v c y 1 − v c Da die Lösung als
Funktion y ( x ) y(x) y ( x ) nicht eindeutig ist, finden wir keine explizite Darstellung.
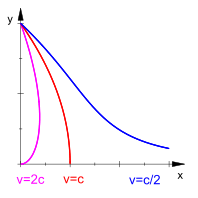
Diskussion der Lösung
Fall
v > c v>c v > c (Hund ist schneller als Fluss)
Für
y → 0 y\to 0 y → 0 ist
y 1 − c v → 0 y^{1- \frac c v}\to 0 y 1 − v c → 0 und damit
x + x 2 + y 2 → 0 x+\sqrt{x^2+y^2}\to 0 x + x 2 + y 2 → 0 , woraus folgt, dass
x → 0 x\to 0 x → 0 . Der Hund kommt also beim Herrchen im Nullpunkt an.
Fall
v < c v<c v < c (Fluss schneller als Hund)
Nun strebt
y 1 − c v → ∞ y^{1- \frac c v}\to \infty y 1 − v c → ∞ für
y → 0 y\to 0 y → 0 . Die linke Seite strebt gegen
2 x 2x 2 x , daher gilt
x → ∞ x\to \infty x → ∞ . Der Hund kommt nicht an und paddelt ewig.
Fall
v = c v=c v = c (Hund und Fluss gleich schnell)
Hier gilt
x + x 2 + y 2 = a x+\sqrt{x^2+y^2}=a x + x 2 + y 2 = a ⟹ \implies ⟹ x 2 + y 2 = ( a − x ) 2 x^2+y^2=(a-x)^2 x 2 + y 2 = ( a − x ) 2 = a 2 − 2 a x + x 2 =a^2-2ax+x^2 = a 2 − 2 a x + x 2 ⟹ \implies ⟹ y 2 = a 2 − 2 a x y^2=a^2-2ax y 2 = a 2 − 2 a x Der Hund paddelt auf einer
Parabel und kommt im
Punkt ( a 2 ; 0 ) \braceNT{\dfrac a 2; 0} ( 2 a ; 0 ) an, muss also noch etwas laufen um zu seinem Herrchen zu kommen.
Jede Wissenschaft bedarf der Mathematik, die Mathematik bedarf keiner.
Jakob I. Bernoulli
Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf
ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld
• Dοrfplatz 25 • 17237 Blankеnsее
• Tel.: 01734332309 (Vodafone/D2) •
Email: cο@maτhepedιa.dе