Ähnlichkeitsdifferentialgleichungen

Eine DGL der Gestalt y′=f (yx)y'=f\, \braceNT{ \dfrac y x} heißt Ähnlichkeitsdifferentialgleichung oder homogene Differentialgleichung (nicht zu verwechseln mit der homogenen linearen Differentialgleichung). Für sie ist y′y' auf allen Ursprungsgeraden y=mxy=mx konstant.
Die DGL kann durch die Substitution z=yxz=\dfrac y x in eine DGL mit getrennten Variablen überführt werden. Mit y=zxy=zx gilt y′=z′x+zy'=z'x+z und damit z′x+z=f(z)z'x+z=f(z) und z′x=f(z)−zz'x=f(z)-z, also
d⁡zf(z)−z=d⁡xx\dfrac {\d z}{f(z)-z}=\dfrac {\d x} x
 
 

Beispiele

y′=9x2+3y22xyy'=\dfrac {9x^2+3y^2}{2xy} =9+3(yx)22yx=\dfrac {9+3\braceNT{\dfrac y x}^2}{2\dfrac y x} =9+3z22z=\dfrac {9+3z^2}{2z}.
d⁡z9+3z22z−z=d⁡xx\dfrac {\d z}{\dfrac {9+3z^2}{2z}-z}=\dfrac {\d x} x   ⟹  2zd⁡z9+z2=d⁡xx\implies \dfrac {2z\d z}{9+z^2}=\dfrac {\d x} x   ⟹  ∫2zd⁡z9+z2=∫d⁡xx\implies\int\limits \dfrac {2z\d z}{9+z^2}=\int\limits\dfrac {\d x} x   ⟹  ln⁡∣9+z2∣=ln⁡∣x∣+C\implies \ln |9+z^2|=\ln|x|+C   ⟹  9+z2=C1x\implies 9+z^2=C_1 x (C1>0C_1>0)   ⟹  z=±C1x−9\implies z=\pm\sqrt{C_1x-9}   ⟹  y=±xC1x−9\implies y=\pm x\sqrt{C_1x-9}

Beispiel 167L

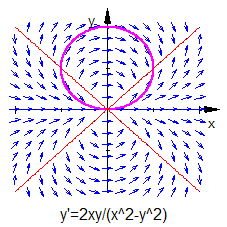
y′=2xyx2−y2=2yx1−(yx)2y'=\dfrac{2xy}{x^2-y^2}=\dfrac {2\dfrac y x} {1-\braceNT{\dfrac y x}^2}
Nach der Substitution z=yxz=\dfrac y x ergibt sich:f(z)−z=2z1−z2−zf(z)-z=\dfrac {2z}{1-z^2}-z =2z−z+z31−z2=\dfrac {2z-z+z^3}{1-z^2} =z3+z1−z2=\dfrac{z^3+z} {1-z^2}.
Für 1f(z)−z=1−z2z3+z\dfrac {1}{f(z)-z}= \dfrac {1-z^2} {z^3+z} =1−z2z(z2+1)= \dfrac {1-z^2} {z(z^2+1)} führen wir eine Partialbruchzerlegung durch mit dem Ansatz: 1−z2z(z2+1)\dfrac {1-z^2} {z(z^2+1)} =Pz+Qz+Rz2+1=\dfrac P z + \dfrac {Qz+R}{z^2+1}   ⟹  1−z2=Pz2+P+Qz2+Rz\implies 1-z^2=Pz^2+P+Qz^2+Rz.
Der Koeffizientenvergleich führt auf P=1P=1, R=0R=0 und −1=P+Q-1=P+Q, also Q=−2Q=-2.
Damit erhalten wird das Integral: ∫(1z−2zz2+1)d⁡z=∫d⁡xx\int\limits\braceNT{ \dfrac 1 z - \dfrac {2z}{z^2+1} }\d z=\int\limits \dfrac {\d x} x   ⟹  ln⁡∣z∣−ln⁡∣z2+1∣=ln⁡∣zz2+1∣=ln⁡∣x∣+C\implies \ln|z|-\ln|z^2+1|=\ln\ntxbraceI{\dfrac z {z^2+1}}=\ln|x|+C   ⟹  zz2+1=±C1x\implies \dfrac z {z^2+1}=\pm C_1x (C1>0C_1>0)
Rücksubstitution: yx(yx)2+1=±C1x\dfrac {\dfrac y x }{\braceNT {\dfrac y x}^2+1}=\pm C_1x   ⟹  y=±C1(x2+y2)\implies y=\pm C_1(x^2+y^2)
Dgl1.png
Mit 2r=1C12r=\dfrac 1 {C_1} ergibt sich: x2+y2±2ry=0 x^2+y^2\pm 2ry=0   ⟹  x2+(y±r)2=r2\implies x^2+(y\pm r)^2 =r^2
Die Lösungskurven sind also Kreise entlang der yy-Achse, deren Radien der y-Koordinate des Mittelpunktes entsprechen.
Für y=±xy=\pm x ist die DGL singulär, was in der Grafik durch das Zusammentreffen der Pfeile der Richtungsfeldes symbolisiert wird.
Diese DGL kann auch einfacher mit der Methode der integrierenden Faktoren gelöst werden (vgl. Beispiel 167W).

Nicht etwa, daß bei größerer Verbreitung des Einblickes in die Methode der Mathematik notwendigerweise viel mehr Kluges gesagt würde als heute, aber es würde sicher viel weniger Unkluges gesagt.

Karl Menger

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

DGL Erster Ordnung