Beispiel 167M

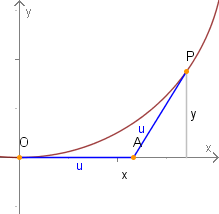
Kreis.png
Wir suchen eine Kurve mit folgender Eigenschaft: Ist AA der Schnittpunkt der Tangente an die Kurve im Punkt PP mit der xx-Achse, so sollen die Strecken OAOA und APAP gleich lang sein.
Der Grafik entnehmen wir nach dem Satz des Pythagoras:
(x−u)2+y2=u2(x-u)^2+y^2=u^2(1)
und
y′=yx−uy'=\dfrac y {x-u}(2)
Wir müssen aus diesen beiden Gleichungen die Größe uu (die nicht konstant ist!) eliminieren.
(1)   ⟹  x2−2ux+u2+y2=u2\implies x^2-2ux+u^2+y^2=u^2   ⟹  u=x2+y22x\implies u=\dfrac {x^2+y^2} {2x}. Dies setzen wir in (2) ein: y′=y(x−x2+y22x)y'=\dfrac y {\braceNT{x-\dfrac {x^2+y^2} {2x}}} =yx2−y22x=\dfrac y {\dfrac {x^2-y^2} {2x}} =2xyx2−y2=\dfrac {2xy} {x^2-y^2}
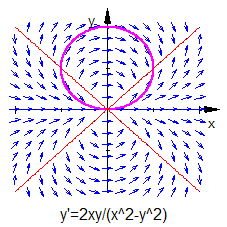
Dgl1.png
Hierbei handelt es sich um eine Ähnlichkeitsdifferentialgleichung, die in Beispiel 167L gelöst wurde. Die allgemeine Lösung hatte die Form x2+(y±r)2=r2x^2+(y\pm r)^2 =r^2
Die Lösungskurven sind also Kreise entlang der yy-Achse, deren Radien der yy-Koordinate des Mittelpunktes entsprechen.
Durch obige Aufgabenstellung wird keine einzelne Kurve eindeutig bestimmt, sondern als Lösung ergibt sich eine ganze Kurvenschar.
Fordern wir, dass die Kurve durch den Punkt (0,1)(0,1) gehen soll, so ergibt sich ein eindeutig bestimmter Kreis mit r=12r=\dfrac 1 2.
 
 

"Offensichtlich" ist das gefährlichste Wort in der Mathematik.

Eric Temple Bell

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

DGL Erster Ordnung