Konvergenzkriterien für uneigentliche Integrale
Satz 16QO (Cauchy-Kriterium)
∀ ε > 0 ∃ c = c ( ε ) ∈ ] a , β [ ∀ u , v ∈ ] c , β [ ∣ ∫ u v f ( x ) d x ∣ < ε \forall \varepsilon>0\;\exists c=c(\varepsilon)\in ]a,\beta[\;\forall u,v\in ]c,\beta[\quad \left|\int\limits_u^v f(x)\; dx\right|<\varepsilon ∀ ε > 0 ∃ c = c ( ε ) ∈ ] a , β [ ∀ u , v ∈ ] c , β [ ∣ ∣ ∣ ∣ u ∫ v f ( x ) d x ∣ ∣ ∣ ∣ < ε Beweis
φ ( t ) : = ∫ a t f ( x ) d x \phi(t):=\int\limits_a^t f(x)\; dx φ ( t ) : = a ∫ t f ( x ) d x Beispiel
Wir zeigen
∫ 0 ∞ sin ( x ) x d x \int\limits_0^\infty \dfrac{\sin (x)}{x}\; dx 0 ∫ ∞ x sin ( x ) d x konvergent Da
lim x → 0 sin ( x ) x = 1 \lim\limits_{x\to 0}\dfrac{\sin(x)}{x}=1 x → 0 lim x sin ( x ) = 1 (
Beispiel 5319B ) bleibt nur
x → ∞ x\to\infty x → ∞ zu betrachten.
Für alle
0 < u < v 0<u<v 0 < u < v gilt:
∣ ∫ u v sin ( x ) x d x ∣ = ∣ ∫ u v 1 x ⎵ = : g ⋅ sin ( x ) ⎵ = : f ´ d x ∣ \left|\int\limits_u^v \dfrac{\sin(x)}{x}\; dx\right|=\left|\int\limits_u^v \underbrace{\dfrac{1}{x}}_{=:g}\cdot\underbrace{\sin(x)}_{=:f´}\; dx\right| ∣ ∣ ∣ ∣ u ∫ v x sin ( x ) d x ∣ ∣ ∣ ∣ = ∣ ∣ ∣ ∣ ∣ ∣ ∣ u ∫ v = : g x 1 ⋅ = : f ´ sin ( x ) d x ∣ ∣ ∣ ∣ ∣ ∣ ∣ = ∣ [ − 1 x cos ( x ) ] u v − ∫ u v 1 x 2 cos x d x ∣ =\left|\left[-\dfrac{1}{x}\cos(x)\right]_u^v-\int\limits_u^v\dfrac{1}{x^2}\cos x\; dx\right| = ∣ ∣ ∣ ∣ [ − x 1 cos ( x ) ] u v − u ∫ v x 2 1 cos x d x ∣ ∣ ∣ ∣ (
partielle Integration )
≤ ∣ cos ( v ) v − cos ( u ) u ∣ + ∫ u v 1 x 2 ∣ cos ( x ) ∣ ⎵ ≤ 1 d x \leq \left|\dfrac{\cos(v)}{v}-\dfrac{\cos(u)}{u}\right|+\int\limits_u^v\dfrac{1}{x^2}\underbrace{\left|\cos(x)\right|}_{\leq 1}\; dx ≤ ∣ ∣ ∣ ∣ v cos ( v ) − u cos ( u ) ∣ ∣ ∣ ∣ + u ∫ v x 2 1 ≤ 1 ∣ cos ( x ) ∣ d x (
Dreiecksungleichung für Integrale )
≤ 1 v − 1 u + ( 1 u − 1 v ) = 2 u \leq\, \dfrac{1}{v}-\dfrac{1}{u}+\left(\dfrac{1}{u}-\dfrac{1}{v}\right)\,=\,\dfrac{2}{u} ≤ v 1 − u 1 + ( u 1 − v 1 ) = u 2 . Sei nun
ε > 0 \varepsilon>0 ε > 0 ; wähle
c : = 2 ε c:=\dfrac{2}{\varepsilon} c : = ε 2 . Dann gilt für
0 < u < v 0<u<v 0 < u < v mit
u > c u>c u > c :
∣ ∫ u v sin ( x ) x d x ∣ ≤ 2 u < 2 c = ε \left|\int\limits_u^v\dfrac{\sin (x)}{x}\; dx\right| \,\leq\, \dfrac{2}{u} \,<\, \dfrac{2}{c}\,=\,\varepsilon ∣ ∣ ∣ ∣ u ∫ v x sin ( x ) d x ∣ ∣ ∣ ∣ ≤ u 2 < c 2 = ε Nach Satz 16QO folgt die Behauptung.
Definition
∫ α β f ( x ) d x \int\limits_\alpha^\beta f(x)\; dx α ∫ β f ( x ) d x heißt
absolut konvergent : ⇔ ∫ α β ∣ f ( x ) ∣ d x :\Leftrightarrow\; \int\limits_\alpha^\beta\left|f(x)\right|\; dx : ⇔ α ∫ β ∣ f ( x ) ∣ d x ist
konvergent .
Satz 16R1
Ist
∫ α β f ( x ) d x \int\limits_\alpha^\beta f(x)\; dx α ∫ β f ( x ) d x absolut
konvergent , so ist es auch
konvergent , und es gilt
∣ ∫ α β f ( x ) d x ∣ ≤ ∫ α β ∣ f ( x ) ∣ d x \left| \int\limits_\alpha^\beta f(x)\; dx\right|\leq \int\limits_\alpha^\beta \left|f(x)\right|\; dx ∣ ∣ ∣ ∣ ∣ α ∫ β f ( x ) d x ∣ ∣ ∣ ∣ ∣ ≤ α ∫ β ∣ f ( x ) ∣ d x .
Beispiel
∫ 0 ∞ sin x x d x \int\limits_0^\infty\dfrac{\sin x}{x} \, dx 0 ∫ ∞ x sin x d x konvergiert nicht absolut, denn
∫ 0 ∞ ∣ sin x ∣ x d x \int\limits_0^\infty \dfrac{|\sin x|}{x} \; dx 0 ∫ ∞ x ∣ sin x ∣ d x konvergiert nicht. Es ist
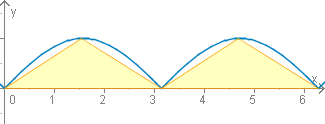
∫ 0 k π ∣ sin x ∣ x d x = ∑ j = 1 k ∫ ( j − 1 ) π j π ∣ sin x ∣ x d x \int\limits_0^{k\pi} \dfrac{|\sin x|}{x} \; dx \;=\; \sum\limits_{j=1}^k \int\limits_{(j-1)\pi}^{j\pi} \dfrac{|\sin x|}{x} \; dx 0 ∫ k π x ∣ sin x ∣ d x = j = 1 ∑ k ( j − 1 ) π ∫ j π x ∣ sin x ∣ d x Abschätzung der Dreiecksfläche unter
sin ( x ) \small\sin(x) sin ( x ) Wir schätzen das
Integral mit Hilfe der Dreiecksflächen unter der
Sinusfunktion ab. Die Größe der Dreiecksfläche ist
A D = π 2 A_D=\dfrac{\pi}{2} A D = 2 π für jedes
k ∈ N k \in \N k ∈ N Es gilt in den einzelnen Teilintervallen
[ ( j − 1 ) π , j π ] [(j-1)\pi,j\pi] [ ( j − 1 ) π , j π ] stets
j π < = x j\pi<=x j π < = x , also
1 j ⋅ π \dfrac{1}{j\cdot\pi} j ⋅ π 1 .
⇒ ∑ j = 1 k ∫ ( j − 1 ) π j π ∣ sin x ∣ x d x \Rightarrow\;\sum\limits_{j=1}^k \int\limits_{(j-1)\pi}^{j\pi} \dfrac{|\sin x|}{x} \; dx ⇒ j = 1 ∑ k ( j − 1 ) π ∫ j π x ∣ sin x ∣ d x ≥ ∑ j = 1 k 1 j ⋅ π ⋅ π 2 \geq \sum\limits_{j=1}^k \dfrac{1}{j \cdot \pi} \cdot \dfrac{\pi}{2} ≥ j = 1 ∑ k j ⋅ π 1 ⋅ 2 π = 1 2 ∑ j = 1 k 1 j → k → ∞ ∞ = \dfrac{1}{2} \sum\limits_{j=1}^k \dfrac{1}{j} \;\xrightarrow{k \to \infty}\; \infty = 2 1 j = 1 ∑ k j 1 k → ∞ ∞ , wegen der Divergenz der
harmonischen Reihe .
Satz 16R2
Es sei
g : [ a , β [ → R g: [a,\beta[\to \R g : [ a , β [ → R mit
∀ t ∈ ] a , β [ \forall t\in ]a,\beta[ ∀ t ∈ ] a , β [ ,
g ∈ R [ a , t ] g\in R[a,t] g ∈ R [ a , t ] riemannintegrierbar .
Majorantenkriterium
Wenn
∀ x ∈ [ a , β [ \forall x\in [a,\beta[ ∀ x ∈ [ a , β [ ∣ f ( x ) ∣ ≤ g ( x ) |f(x)|\leq g(x)\, ∣ f ( x ) ∣ ≤ g ( x ) und
∫ a β g ( x ) d x \int\limits_a^\beta g(x)\; dx a ∫ β g ( x ) d x konvergent . Dann ist
∫ a β f ( x ) d x \int\limits_a^\beta f(x)\; dx a ∫ β f ( x ) d x absolut
konvergent , und es gilt
∫ a β ∣ f ( x ) ∣ d x ≤ ∫ a β g ( x ) d x \int\limits_a^\beta |f(x)|\; dx\leq\int\limits_a^\beta g(x)\; dx a ∫ β ∣ f ( x ) ∣ d x ≤ a ∫ β g ( x ) d x Minorantenkriterium
Wenn
∀ x ∈ [ a , β [ \forall x\in [a,\beta[ ∀ x ∈ [ a , β [ f ( x ) ≥ g ( x ) ≥ 0 f(x)\geq g(x)\geq 0 f ( x ) ≥ g ( x ) ≥ 0 und
∫ a β g ( x ) d x \int\limits_a^\beta g(x)\; dx a ∫ β g ( x ) d x divergent .
Dann ist auch
∫ a β f ( x ) d x \int\limits_a^\beta f(x)\; dx a ∫ β f ( x ) d x divergent .
Jede mathematische Formel in einem Buch halbiert die Verkaufszahl dieses Buches.
Stephen Hawking
Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf
ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld
• Dοrfplatz 25 • 17237 Blankеnsее
• Tel.: 01734332309 (Vodafone/D2) •
Email: cο@maτhepedιa.dе