Die Kettenlinie

Die Kettenlinie (auch Katenoide) beschreibt die Kurvenform, die eine Kette oder eines Seil annimmt, das nur unter Einwirkung der Schwerkraft aufgehängt wird.

Herleitung der Differentialgleichung

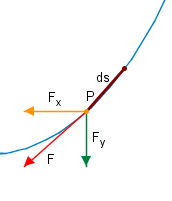
Kettenlinie.png
In einem Punkt PP gilt y′=d⁡yd⁡x=FyFxy'=\dfrac {\d y} {\d x}=\dfrac {F_y}{F_x}   ⟹  \implies Fy=y′FxF_y=y'F_x. Da keine horizontalen Verformungen auftreten können, muss die xx-Komponente der Kraft konstant sein, also
(Fy)′=Fxy′′(F_y)'=F_xy''(1)
Ist nun qq das Gewicht des Seils pro Länge, so gilt d⁡Fy=qd⁡s\d F_y=q\d s.
Wegen d⁡s=(d⁡x)2+(d⁡y)2\d s=\sqrt{(\d x)^2+(\d y)^2} =1+y′2d⁡x=\sqrt{1+y'^2}\d x gilt (Fy)′=q1+y′2(F_y)'=q \sqrt{1+y'^2}. und mit (1):
Fxy′′=q1+y′2F_xy''=q \sqrt{1+y'^2}
Setzen wir k=qFxk=\dfrac q {F_x} so erhalten wir

Formel 168D (Differentialgleichung der Kettenlinie)

y′′=k1+y′2y''=k \sqrt{1+y'^2}

Lösung der DGL

Die DGL enthält nur die erste und zweite Ableitung kann also mittels der Substitution z=y′z=y' auf eine Differentialgleichung erster Ordnung zurückgeführt werden:
z′=k1+z2z'=k \sqrt{1+z^2}
Diese DGL lässt sich durch Trennung der Variablen lösen: d⁡z1+z2=kd⁡x\dfrac {\d z}{\sqrt{1+z^2}}=k\d x
  ⟹  ∫d⁡z1+z2=k∫d⁡x\implies \int\limits\dfrac {\d z}{\sqrt{1+z^2}}=k\int\limits \d x
  ⟹  ln⁡∣z+z2+1∣=arcsinhz=kx+C\implies \ln\ntxbraceI{z+\sqrt{z^2+1}}=\mathrm{arcsinh }z= kx+C (Beispiel 167H; Areafunktionen)
  ⟹  y′=sinh⁡(kx+C)\implies y'=\sinh(kx+C)
  ⟹  y=1kcosh⁡(kx+C)+D\implies y= \dfrac 1 k \cosh (kx+C)+D =12k(e⁡kx+C+e⁡−kx−C)+D=\dfrac 1 {2 k } (\e^{kx+C} +\e^{-kx-C})+D (Satz 5318E)
Die Form der Kettenlinie wird also durch den Hyperbelkosinus beschrieben.
 
 

Scherzhafte Beispiele haben manchmal größere Bedeutung als ernste.

Michael Stifel

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Gewöhnliche Differentialgleichungen