Sukzessive Approximation

Die sukzessive Approximation (schrittweise Annäherung) ist ein Verfahren zur näherungsweisen Lösung von Differentialgleichungen erster Ordnung.
Dazu benutzen wir die folgende Identität

Satz 168O

Sei das folgende Anfangswertproblem gegeben y′=f(x,y)y'=f(x,y) und y(x0)=y0y(x_0)=y_0. Dies ist gleichwertig zu
y(x)=y0+∫x0xf(t,y(t))d⁡ty(x)=y_0+\int\limits_{x_0}^x f(t,y(t)) \d t.(1)

Beweis

"  ⟹  \implies": y′=f(x,y)y'=f(x,y) wird von x0x_0 bis xx integriert. ∫x0xy′(t)d⁡t=∫x0xf(t,y(t))d⁡t\int\limits_{x_0}^xy'(t)\d t=\int\limits_{x_0}^xf(t,y(t)) \d t ergibt nach dem Hauptsatz der Differential- und Integralrechnung: y(x)−y0=∫x0xf(t,y(t))d⁡ty(x)-y_0=\int\limits_{x_0}^xf(t,y(t)) \d t, also
y(x)=y0+∫x0xf(t,y(t))d⁡ty(x)=y_0+\int\limits_{x_0}^xf(t,y(t)) \d t
⇐\Leftarrow: y(x0)=y0+∫x0x0f(t,y(t))d⁡t=y0y(x_0)=y_0+\int\limits_{x_0}^{x_0} f(t,y(t)) \d t=y_0
Differenzieren wir (1), ergibt sich sofort y′=f(x,y)y'=f(x,y). □\qed
Für das Verfahren benutzen wir den Startwert y(x0)=y0y(x_0)=y_0 und integrieren (1) für den ersten Näherungswert y1y_1.
y1(x)=y0+∫x0xf(t,y0)d⁡ty_1(x)=y_0+\int\limits_{x_0}^x f(t,y_0) \d t
Diesen nehmen wir als Startwert für die erneute Integration und erhalten den nächsten Wert. Allgemein berechnen wir den n+1n+1-ten Näherungswert durch
yn+1(x)=y0+∫x0xf(t,yn)d⁡ty_{n+1}(x)=y_0+\int\limits_{x_0}^x f(t,y_n) \d t

Beispiel

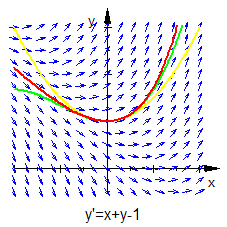
y′=x+y−1y'=x+y-1; y(0)=1y(0)=1
y1(x)=1+∫0x(t+1−1)d⁡ty_1(x)=1+\int\limits_0^x(t+1-1)\d t =1+∫0xtd⁡t=1+\int\limits_0^xt\d t =1+x22=1+\dfrac{x^2} 2.
y2(x)=1+∫0x(t+1+t22−1)d⁡ty_2(x)=1+\int\limits_0^x(t+1+\dfrac{t^2} 2-1)\d t =1+∫0xt+t22d⁡t=1+\int\limits_0^x t+\dfrac{t^2} 2\d t =1+x22+x36=1+\dfrac{x^2} 2+\dfrac{x^3} 6 =1+x22+x36=1+\dfrac{x^2} 2+\dfrac{x^3} 6
BspSuk.png
Die Grafik zeigt die wahre Lösungskurve (rot) sowie y1y_1 (gelb) und y2y_2 (grün).
Die lineare Differentialgleichung ist in Beispiel 168P gelöst worden.
 
 

Ein Mathematiker, der nicht irgendwie ein Dichter ist, wird nie ein vollkommener Mathematiker sein.

Karl Weierstraß

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Gewöhnliche Differentialgleichungen