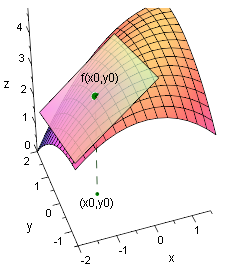
Geometrische Deutung der totalen Ableitung
Für eine
Funktion f : R 2 → R f:\R^2\to\R f : R 2 → R können wir uns die
totale Ableitbarkeit veranschaulichen. Sie bedeutet die Existenz einer Tangentialebene an den
Punkt ( x 0 , y 0 , f ( x 0 , y 0 ) ) (x_0,y_0,f(x_0,y_0)) ( x 0 , y 0 , f ( x 0 , y 0 ) ) .
lim ( h , k ) → 0 f ( x 0 + h , y 0 + k ) − f ( x 0 , y 0 ) − ( c ⋅ h + d ⋅ k ) h 2 + k 2 = 0 \lim_{(h,k)\to 0}\dfrac{f(x_0+h,y_0+k)-f(x_0,y_0)-(c\cdot h+d\cdot k)} {\sqrt{h^2+k^2}} =0 lim ( h , k ) → 0 h 2 + k 2 f ( x 0 + h , y 0 + k ) − f ( x 0 , y 0 ) − ( c ⋅ h + d ⋅ k ) = 0 Da der
Zähler für kleine Vektoren
( h , k ) (h,k) ( h , k ) nahe bei 0 liegen muss ergibt sich:
f ( x 0 + h , y 0 + k ) ≈ f ( x 0 , y 0 ) + c ⋅ h + d ⋅ k f(x_0+h,y_0+k)\approx f(x_0,y_0)+c\cdot h+d\cdot k f ( x 0 + h , y 0 + k ) ≈ f ( x 0 , y 0 ) + c ⋅ h + d ⋅ k Mit
x = x 0 + h x=x_0+h x = x 0 + h und
y = y 0 + k y=y_0+k y = y 0 + k :
f ( x , y ) ≈ f ( x 0 , y 0 ) + c ⋅ ( x − x 0 ) + d ⋅ ( y − y 0 ) f(x,y)\approx f(x_0,y_0)+c\cdot (x-x_0)+d\cdot (y-y_0) f ( x , y ) ≈ f ( x 0 , y 0 ) + c ⋅ ( x − x 0 ) + d ⋅ ( y − y 0 ) ,
und da
c = ∂ f ∂ x ( x 0 , y 0 ) c=\dfrac {\partial f}{\partial x} (x_0,y_0) c = ∂ x ∂ f ( x 0 , y 0 ) und
d = ∂ f ∂ y ( x 0 , y 0 ) d=\dfrac {\partial f}{\partial y} (x_0,y_0) d = ∂ y ∂ f ( x 0 , y 0 ) aber gerade die
partiellen Ableitungen sind:
f ( x , y ) ≈ f ( x 0 , y 0 ) + ( x − x 0 ) ⋅ ∂ f ∂ x ( x 0 , y 0 ) f(x,y)\approx f(x_0,y_0)+(x-x_0)\cdot\dfrac {\partial f}{\partial x} (x_0,y_0) f ( x , y ) ≈ f ( x 0 , y 0 ) + ( x − x 0 ) ⋅ ∂ x ∂ f ( x 0 , y 0 ) + ( y − y 0 ) ⋅ ∂ f ∂ y ( x 0 , y 0 ) + (y-y_0)\cdot\dfrac {\partial f}{\partial y} (x_0,y_0) + ( y − y 0 ) ⋅ ∂ y ∂ f ( x 0 , y 0 ) ,
Damit erhalten wir als Gleichung der Tangentialebene an
f f f im
Punkt ( x 0 , y 0 , f ( x 0 , y 0 ) ) (x_0,y_0,f(x_0,y_0)) ( x 0 , y 0 , f ( x 0 , y 0 ) ) :
T ( x , y ) = f ( x 0 , y 0 ) + ( x − x 0 ) ⋅ ∂ f ∂ x ( x 0 , y 0 ) T(x,y)=f(x_0,y_0)+(x-x_0)\cdot\dfrac {\partial f}{\partial x} (x_0,y_0) T ( x , y ) = f ( x 0 , y 0 ) + ( x − x 0 ) ⋅ ∂ x ∂ f ( x 0 , y 0 ) + ( y − y 0 ) ⋅ ∂ f ∂ y ( x 0 , y 0 ) + (y-y_0)\cdot\dfrac {\partial f}{\partial y} (x_0,y_0) + ( y − y 0 ) ⋅ ∂ y ∂ f ( x 0 , y 0 ) Jede Wissenschaft bedarf der Mathematik, die Mathematik bedarf keiner.
Jakob I. Bernoulli
Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf
ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld
• Dοrfplatz 25 • 17237 Blankеnsее
• Tel.: 01734332309 (Vodafone/D2) •
Email: cο@maτhepedιa.dе