Beispiele zur Poisson-Verteilung
Die Poisson-Verteilung ist eine typische Verteilung für die Zahl von Phänomenen, die innerhalb einer Einheit auftreten.
So wird sie häufig dazu benutzt, zeitliche Ereignisse zu beschreiben. Gegeben sind ein zufälliges Ereignis, das durchschnittlich einmal in einem zeitlichen Abstand stattfindet, sowie ein zweiter Zeitraum , auf den dieses Ereignis bezogen werden soll.
Die Poissonverteilung mit gibt die Wahrscheinlichkeit an, dass im Zeitraum genau Ereignisse stattfinden. Anders ausgedrückt ist die mittlere Auftretenshäufigkeit eines Ereignisses.
Beispiel 1
Ein Kaufhaus wird an einem Samstag durchschnittlich alle 10 Sekunden von einem Kunden betreten. Werden nun im Takt von einer Minute bzw. 60s die Personen gezählt, so würde man im Mittel 6 Personen erwarten ( = 1Person/10s *60s = 6), die das Kaufhaus betreten. gibt die Wahrscheinlichkeit dafür an, dass in der nächsten Minute genau Kunden das Kaufhaus betreten.
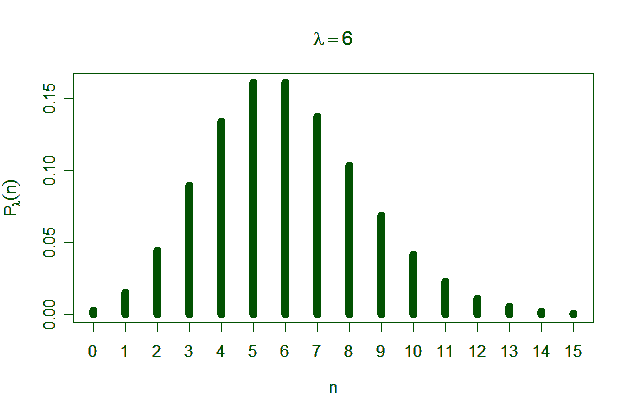
Poisson-Verteilung mit =6.
Mit einer Wahrscheinlichkeit von fast 5% betreten genau 2 Personen in einer Minute das Kaufhaus. Mit einer Wahrscheinlichkeit von fast 92% treten 0 bis 9 Personen (aufsummiert) ein. Die Wahrscheinlichkeit, dass mehr als 9 Personen in einer Minute eintreten, ist folglich 8% .
Beispiel 2
In der Natur folgt zum Beispiel die zeitliche Abfolge radioaktiver Zerfälle einzelner Atome der Poisson-Statistik.
Beispiel 3
Die Blitzhäufigkeit in Deutschland beträgt 10 Einschläge pro km² = 0,1 Einschläge pro ha und Jahr. Wie groß ist die Wahrscheinlichkeit, dass es in einer Parzelle von 1 ha zu Blitzeinschlägen in einem Jahr kommt?
Einschläge pro Hektar und Jahr.
- (kein Einschlag im betrachteten Jahr): 90%
- (ein Einschlag im betrachteten Jahr): 9%
- (zwei Einschläge im betrachteten Jahr): 0,5%
- (drei Einschläge im betrachteten Jahr): 0,02%
Statistisch ist es nicht verwunderlich, wenn ein Blitz innerhalb von 200 Jahren zweimal am gleichen Ort einschlägt, wobei es außerordentlich unwahrscheinlich ist, den Ort voraussagen zu können (Siehe hierzu auch Geburtstagsproblem).
Beispiel 4
Wenn das zeitliche Eintreffen seltener Ereignisse einen Poisson-Prozess bildet, folgen die Zeitintervalle zwischen den Ereignissen einer Exponentialverteilung. Ein Anwendungsbeispiel für die Simulation poissonverteilter Zufallszahlen findet sich unter Verteilung von Zufallszahlen.
Beispiel 5

Zufällig auf dem Boden verstreute Reiskörner.
Das Bild rechts zeigt N=66 Reiskörner, die zufällig auf 1/p=49 Quadrate verteilt wurden. Die Felder enthalten n=0,..5 Reiskörner. Der Vergleich zwischen Experiment und berechneter Poissonverteilung P(n) ( = N*p = 66/49 = 1,33) zeigt eine gute Übereinstimmung:
n gezählt p(n)*49 0 16 13 1 14 17 2 10 11 3 6 5 4 1 2 5 2 0.5
Ein Mathematiker, der nicht irgendwie ein Dichter ist, wird nie ein vollkommener Mathematiker sein.
Karl Weierstraß
Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf
ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld
• Dοrfplatz 25 • 17237 Blankеnsее
• Tel.: 01734332309 (Vodafone/D2) •
Email: cο@maτhepedιa.dе