Aufgabe 16G5

da002.png
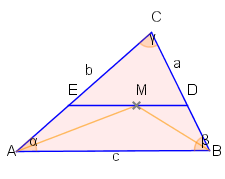
Im Dreieck ΔABC\Delta ABC sei MM der Mittelpunkt der Winkelhalbierenden. ED‾\overline{ED} sei die Parallele zu AB‾\overline{AB} durch MM. Man drücke die Länge von ED‾\overline{ED} durch die Längen der Dreiecksseiten aa, bb und cc aus.
da002l.png

Lösung

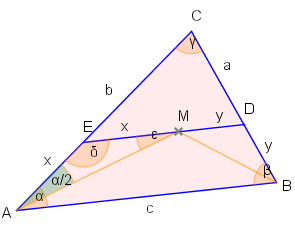
Wir bezeichnen x=EM‾x=\overline{EM} und y=MD‾y=\overline{MD}. Die gesuchte Größe ist dann x+yx+y.
Zuerst zeigen wir, dass auch AE‾=EM‾\overline{AE}=\overline{EM}.
Der Winkel δ=∠AEM\delta=\angle AEM ist Gegenwinkel zu α\alpha, also gilt δ=180°−α\delta=180°-\alpha. Im Dreieck ΔAME\Delta AME gilt auf Grund des Innenwinkelsatzes: α2+180°−α+ϵ=180°\dfrac{\alpha}{2}+180°-\alpha+\epsilon=180°. Damit erhalten wir ϵ=α2\epsilon=\dfrac{\alpha}{2}. Da gleichgroßen Winkeln gleichlange Seiten gegenüberliegen, ist x=EM‾=AE‾x=\overline{EM}=\overline{AE}.
Analog kann man schließen y=DM‾=DB‾y=\overline{DM}=\overline{DB}.
Da ED‾∣∣AB‾\overline{ED}||\overline{AB} können wir jetzt den Strahlensatz anwenden und erhalten die beiden Beziehungen b−xx+y=bc\dfrac{b-x}{x+y}=\dfrac{b}{c} und a−yx+y=ac\dfrac{a-y}{x+y}=\dfrac{a}{c}.
Und nach Beseitigung der Brüche: (b−x)c=b(x+y)=bx+by(b-x)c=b(x+y)=bx+by und (a−y)c=a(x+y)(a-y)c=a(x+y).
Wir stellen die erste Gleichung nach yy um und erhalten:
y=(b−x)c−bxb=c−x−cxby=\dfrac{(b-x)c-bx}{b}=c-x-\dfrac{cx}b.
Dies setzen wir in die zweite Gleichung ein: (a−c+x+cxb)c=a(x+c−x−cxb)=a(c−cxb)(a-c+x+\dfrac{cx}{b})c=a(x+c-x-\dfrac{cx}b)=a(c-\dfrac{cx}b), also ac−c2+cx+c2xb=ac−acxbac-c^2+cx+\dfrac{c^2x}{b}=ac-\dfrac{acx}{b} und schließlich: cx+c2xb+acxb=c2cx+\dfrac{c^2x}{b}+\dfrac{acx}{b}=c^2.
Multiplizieren wir die Gleichung mit bb: bcx+c2x+acx=c2bbcx+c^2x+acx=c^2b. Jetzt können wir auf der linken Seite cxcx ausklammern: cx(a+b+c)=c2bcx(a+b+c)=c^2b und damit:
x=bca+b+cx=\dfrac{bc}{a+b+c}
Gehen wir jetzt von b−xx+y=bc\dfrac{b-x}{x+y}=\dfrac{b}{c} aus, und setzen in x+y=c(b−x)b=c−cbxx+y=\dfrac{c(b-x)}b=c-\dfrac cbx das erhaltene Ergebnis für x ein: x+y=c−cb⋅bca+b+cx+y=c-\dfrac cb\cdot \dfrac{bc}{a+b+c} == ca+cb+c2−c2a+b+c\dfrac{ca+cb+c^2-c^2}{a+b+c} und schließlich die Lösung:
x+y=c(a+b)a+b+cx+y=\dfrac{c(a+b)}{a+b+c}
 
 

Es ist unglaublich, wie unwissend die studirende Jugend auf Universitäten kommt, wenn ich nur 10 Minuten rechne oder geometrisire, so schläft 1/4 derselben sanft ein.

Georg Christoph Lichtenberg

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Das Dreieck