Aufgabe 16G6

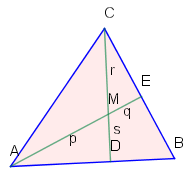
da6.png
Im Dreieck ΔABC\Delta ABC seien die beiden Höhen CD‾\overline{CD} und AE‾\overline{AE} gegeben. Diese schneiden sich im Punkt MM. Es seien p=AM‾p=\overline{AM}, q=ME‾q=\overline{ME}, r=CM‾r=\overline{CM} und s=MD‾s=\overline{MD}. Man zeige, dass dann pq=rspq=rs gilt.

Lösung

Die Dreiecke ΔADM\Delta ADM und ΔCME\Delta CME sind ähnlich, denn sie stimmen in einem rechten Winkel und dem Scheitelwinkel ∠AMD=∠CME\angle AMD = \angle CME überein. Damit können wir den Strahlensatz anwenden und erhalten:
qs=rp\dfrac qs = \dfrac rp,
woraus sich unmittelbar die Behauptung pq=rspq=rs ergibt.
 
 

Ich glaube, daß es, im strengsten Verstand, für den Menschen nur eine einzige Wissenschaft gibt, und diese ist reine Mathematik. Hierzu bedürfen wir nichts weiter als unseren Geist.

Georg Christoph Lichtenberg

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Das Dreieck