Aufgabe 16G3

Im rechtwinkligen Dreieck ΔABC\Delta ABC sei GG ein beliebiger Punkt auf der Höhe hh. Der Schnittpunkt der Parallele zu BC‾\overline{BC} durch GG mit der Seite AB‾\overline{AB} sei HH. Die Gerade durch AA und GG schneide CH‾\overline{CH} im Punkt II.
Man zeige, dass AI‾⊥CH‾\overline{AI} \perp \overline{CH}.
(Der rechte Winkel liegt bei CC)

Lösung

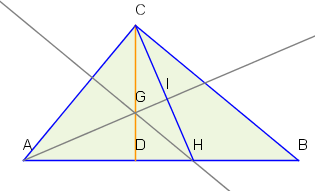
da001.png
Wir betrachten das Dreieck ΔAHC\Delta AHC. In diesem ist CD‾\overline{CD} auch eine Höhe. Da BC‾∣∣GH‾\overline{BC} || \overline{GH} ist, gilt GH‾⊥AC‾\overline{GH} \perp \overline{AC}. Also ist GH‾\overline{GH} auch Höhe im Dreieck ΔAHC\Delta AHC. Damit ist GG der Schnittpunkt der Höhen im Dreieck ΔAHC\Delta AHC.
Die Strecke AI‾\overline{AI} geht nach der Aufgabenstellung durch den Höhenschnittpunkt GG. Damit muss AI‾\overline{AI} auch Höhe im Dreieck ΔAHC\Delta AHC sein. Das bedeutet aber: AI‾⊥CH‾\overline{AI} \perp \overline{CH}
 
 

Ich stimme mit der Mathematik nicht überein. Ich meine, daß die Summe von Nullen eine gefährliche Zahl ist.

Stanislaw Jerzy Lec

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Das Dreieck