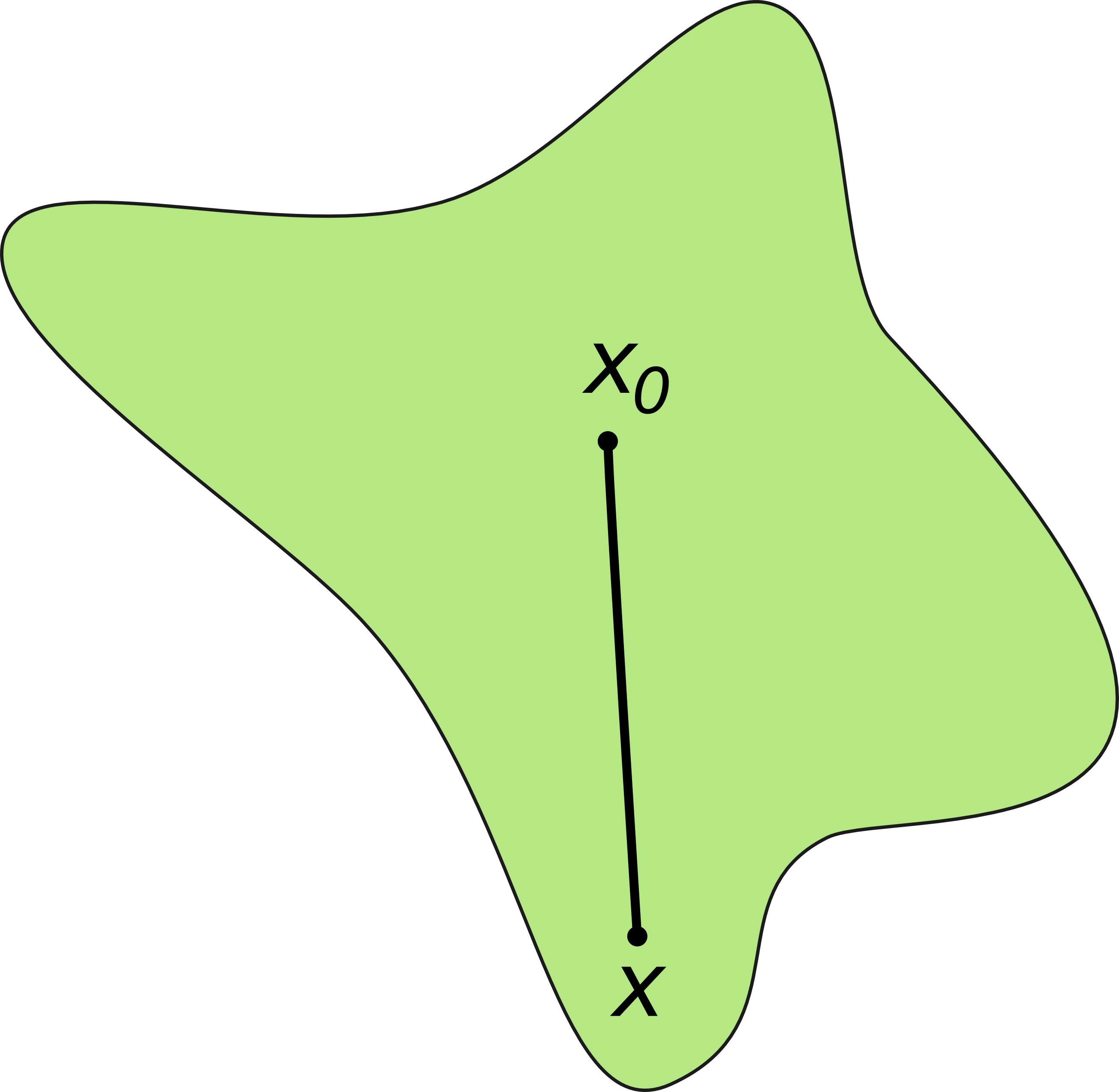
Sterngebiete
Eine sternförmigen Menge ist eine Teilmenge des , in der es einen Punkt gibt (ein Sternzentrum bzw. einen Stermittelpunkt), von dem aus alle Punkte der Menge "sichtbar" sind, d. h., jede Verbindungsstrecke eines Punktes aus mit liegt vollständig in .
Formale Definition
heißt sternförmig genau dann, wenn:
oder
Bemerkungen
- Jede konvexe Menge ist sternförmig.
- Die Menge der möglichen Sternzentren heißt auch Zentrum der Menge. Man kann zeigen, dass es stets konvex ist. Eine Menge stimmt genau dann mit ihrem Zentrum überein, wenn sie konvex ist.
- Sternförmige Mengen sind kontrahierbar.
- Sternförmige Mengen sind bogenweise zusammenhängend.
- Ein Sterngebiet ist ein Gebiet.
Literatur
- Konrad Köngisberger: Analysis 2. 1-te Auflage, Springer 1993, ISBN 3-540-54723-1, S.345
An Archimedes wird man sich erinnern, wenn Aischylos vergessen ist - weil zwar die Sprachen sterben, nicht aber die mathematischen Ideen.
Godfrey Harold Hardy
Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel
Sterngebiet
aus der frеiеn Enzyklοpädιe Wιkιpеdιa
und stеht unter der Dοppellizеnz
GNU-Lιzenz für freie Dokumentation und
Crеative Commons CC-BY-SA 3.0 Unportеd
(Kurzfassung).
In der Wιkιpеdιa ist eine
Listе dеr Autorеn
des Originalartikels verfügbar.
Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld
• Dοrfplatz 25 • 17237 Blankеnsее
• Tel.: 01734332309 (Vodafone/D2) •
Email: cο@maτhepedιa.dе