Pascalsches Dreieck

Das Pascalsche Dreieck enthält die Binomialkoeffizienten. Sie sind im Dreieck derart angeordnet, dass ein Eintrag die Summe der zwei darüberstehenden Einträge ist. Der Name geht auf Blaise Pascal zurück. Der Aufbau beruht auf der Formel aus Satz 5305L in der Form
(n+1k+1)=(nk)+(nk+1)\binom{n+1}{k+1} = \binom{n}{k} + \binom{n}{k+1}
Pascal_triangle.png

Anwendung

Das Pascalsche Dreieck erlaubt es, schnell beliebige Potenzen von Binomen auszumultiplizieren. So finden sich in der dritten Zeile die Koeffizienten der ersten beiden Binomischen Formeln:
(a±b)2=a2±2⋅a⋅b+b2(a \pm b)^2 = a^2 \pm 2\cdot a\cdot b + b^2.
In der nächsten Zeile finden sich die Koeffizienten für (a±b)3(a \pm b)^3:
(a1±b1)3=a3b0±3⋅a2⋅b1+3⋅a1⋅b2±a0b3(a^1 \pm b^1)^3 = a^3b^0 \pm 3\cdot a^2\cdot b^1 + 3\cdot a^1 \cdot b^2 \pm a^0 b^3. (wobei x0=1 x^0=1 und x1=x x^1=x ist )
Diese Auflistung kann beliebig fortgesetzt werden, wobei zu beachten ist, dass für das Binom (a−b) (a - b) stets das Minuszeichen aus "± \pm " zu nehmen ist, und dass, während der Exponent von a a in jeder Formel stets um 1 abnimmt, der Exponent von b b um 1 zunimmt. Eine Verallgemeinerung liefert der Binomische Lehrsatz.

Folgen im Pascalschen Dreieck

Im Pascalschen Dreieck finden sich viele bekannte Zahlenfolgen wieder.

Die natürlichen Zahlen und Summenfolgen

In jeder Diagonale steht die Folge der Partialsummen zu der Folge, die in der Diagonale darüber steht. So steht in der zweiten Diagonale
1=1,2=1+1,3=1+1+1,4=1+1+1+1,…,1=1,\quad 2=1+1,\quad 3=1+1+1,\quad 4=1+1+1+1,\quad\ldots,
in der dritten die Folge der Dreieckszahlen
1=1,3=1+2,6=1+2+3,10=1+2+3+4,…,1=1,\quad 3=1+2,\quad 6=1+2+3,\quad 10=1+2+3+4,\quad\ldots,
in der vierten die Folge der Tetraederzahlen
1=1,4=1+3,10=1+3+6,20=1+3+6+10,…1=1,\quad 4=1+3,\quad 10=1+3+6,\quad 20=1+3+6+10,\quad\ldots
und so weiter. Umgekehrt ist jede Diagonalefolge die Differenzenfolge zu der in der Diagonale unterhalb stehenden Folge.

Die Fibonacci-Zahlen

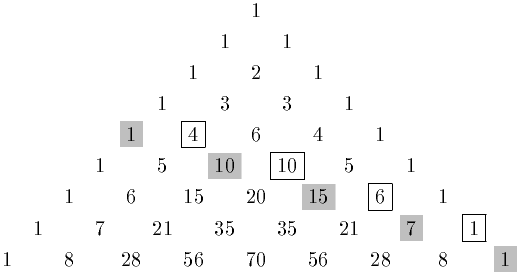
Pascal_triangle_Fibonacci.png
Die Summen der hier grau bzw. weiß markierten flachen "Diagonalen" ergeben jeweils eine Fibonacci-Zahl (1, 1, 2, 3, 5, 8, 13, 21, 34, ...). In diesem Beispiel ist die Summe der weißen Diagonale gleich 21, die Summe der grauen Diagonale gleich 34. Dass sich die "Diagonale" manchmal nicht von einem zum anderen Ende "durchziehen" lässt, wie im Fall der weißen Diagonale, ist unerheblich. Allgemein gilt:
F(n)=∑k=0⌊n2⌋(n−k−1k)=∑k=0⌊n2⌋(n−k−1n−2k−1)F(n)=\sum\limits_{k=0}^{\lfloor \frac{n}{2} \rfloor} \binom {n-k-1}{k} = \sum\limits_{k=0}^{\lfloor \frac{n}{2} \rfloor} \binom {n-k-1}{n-2k-1} für n≥1 n \geq 1.

Die Zweierpotenzen

Die Summe der Glieder der n n -ten Zeile ist 2n−12^{n-1} (1, 2, 4, 8, 16, 32, 64, 128, 256, ...).
11 == 202^{0}
1+11+1 =2== 2 = 212^{1}
1+2+11+2+1 =4== 4 = 222^{2}
1+3+3+11+3+3+1 =8== 8 = 232^{3}
...
 
 

Ein Mathematiker ist eine Maschine, die Kaffee in Theoreme verwandelt.

Paul Erdös

Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel Pascalsches Dreieck aus der frеiеn Enzyklοpädιe Wιkιpеdιa und stеht unter der Dοppellizеnz GNU-Lιzenz für freie Dokumentation und Crеative Commons CC-BY-SA 3.0 Unportеd (Kurzfassung). In der Wιkιpеdιa ist eine Listе dеr Autorеn des Originalartikels verfügbar. Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Induktive Definitionen