Bogenlänge

Bogenlaenge.png
Um die Länge eines Kurvenbogens der Funktion y=f(x)y=f(x) im Intervall [a,b][a,b] zu berechnen, zerlegen wir das Intervall [a,b][a,b] durch Einfügen von Teilpunkten xix_i (i=0,…,n)(i=0,\ldots ,n) Dabei soll a=x0<x1<x2<…<xn=ba=x_0<x_1<x_2<\ldots<x_n=b gelten.
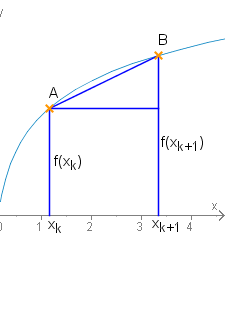
Für zwei solche Teilpunkte xkx_k und xk+1x_{k+1} wird der Kurvenbogen durch die Strecke AB‾\overline{AB} angenähert (siehe Graphik). Dabei gilt
l(AB‾)=(f(xk+1)−f(xk))2+(xk+1−xk)2l(\overline{AB})=\sqrt{(f(x_{k+1})-f(x_{k}) )^2 +(x_{k+1}-x_k)^2 }
und für die Länge lnl_n aller Streckensegmente des Kurvenbogens über das gesamte Intervall [a,b][a,b]:
ln=∑k=0n−1(f(xk+1)−f(xk))2+(xk+1−xk)2l_n=\sum\limits_{k=0}^{n-1} \sqrt{(f(x_{k+1})-f(x_{k}) )^2 +(x_{k+1}-x_k)^2 }.
Nun formen wir dies zu
ln=∑k=0n−11+(f(xk+1)−f(xk)xk+1−xk)2(xk+1−xk)l_n=\sum\limits_{k=0}^{n-1} {\sqrt{1+{\braceNT{\dfrac{ f(x_{k+1})-f(x_{k})}{x_{k+1}-x_k}}}^2 } (x_{k+1}-x_k)}
um. Jetzt lassen wir die Länge der einzelnen Teilintervalle gegen 0 gehen und erhalten für die Länge ll des Kurvenbogens das Integral:
 
 

Formel 15W1 (Bogenlänge einer Kurve)

l=∫ab1+[f ′(x)]2d⁡xl=\int\limits_a^b {\sqrt {1+[f\, '(x)]^2}\d x}
Existiert dieses bestimmte Integral, so heißt die Kurve rektifizierbar.

Nach unserer bisherigen Erfahrung sind wir zum Vertrauen berechtigt, dass die Natur die Realisierung des mathematisch denkbar Einfachsten ist.

Albert Einstein

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Integralrechnung