Die Traktrix

Die Traktrix oder Schleppkurve (von lat. trahere=ziehen) beschreibt die Bewegung eines Punktes, der mittels einer Stange etc. gezogen wird.

Herleitung der Gleichung

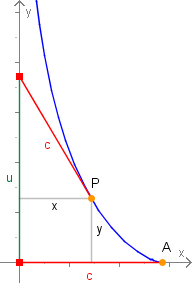
Traktrix.png
Im Punkt A=(c,0)A=(c,0) liegt ein Stein o.ä. Dieser ist durch eine Schnur mit den Nullpunkt verbunden. Auf welcher Kurve bewegt sich der Stein, wenn wir das Ende der Schnur entlang der yy-Achse nach oben bewegen?
Für einen beliebigen Punkt P(x;y)P(x;y) auf der Kurve gilt nach dem Satz des Pythagoras:
(u−y)2+x2=c2(u-y)^2+x^2=c^2
Die Schnur greift tangential an die Kurve an, daher ist y′=u−yxy'=\dfrac {u-y} x, also (u−y)2=y′2x2(u-y)^2=y'^2x^2. Setzen wir dies ein: y′2x2=c2−x2y'^2x^2=c^2-x^2, also
y′=±c2−x2xy'=\pm\dfrac {\sqrt{c^2-x^2}} x
(Für den in der Grafik dargestellten Abschnitt gilt das negative Vorzeichen, da die Anstiege der Tangenten negativ sind.)
In Beispiel 167J haben wir das entsprechende Integral gelöst und erhalten: y(x)=±c2−x2 ∓cln⁡c+c2−x2x+Cy(x)=\pm\sqrt {c^2- x^2} \, \mp c\ln \dfrac {c+\sqrt {c^2- x^2}} x+C.
Da nach Voraussetzung y(c)=0y(c)=0 gelten soll, kann die Integrationskonstante mit C=0C=0 bestimmt werden.

Gleichung der Traktrix

y(x)=±c2−x2 ∓cln⁡c+c2−x2xy(x)=\pm\sqrt {c^2- x^2} \, \mp c\ln \dfrac {c+\sqrt {c^2- x^2}} x
 
 

Es gibt jedoch noch einen anderen Grund für die hohe Wertschätzung der Mathematik; sie allein bietet den Naturwissenschaften ein gewisses Maß an Sicherheit, das ohne Mathematik nicht erreichbar wäre.

Albert Einstein

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Integralrechnung