Klassifikation der Lösungen

eines linearen homogenen 2x2 Differentialgleichungssystems mit konstanten Koeffizienten

Bei der Diskussion des linearen homogenen Differentialgleichungssystems
x′(t)=ax(t)+by(t)x'(t)=ax(t)+by(t)
y′(t)=cx(t)+dy(t)y'(t)=cx(t)+dy(t)
wollen wir die Lösung als Ortskurve des R2\R^2 auffassen. Es gibt stets eine triviale Lösung x(t)=y(t)=0x(t)=y(t)=0, der Punkt bewegt sich nicht und verharrt im Nullpunkt in einer Gleichgewichtslage. Bei der weiteren Untersuchung interessieren wir uns für das Verhalten in der Nähe dieses Gleichgewichtspunktes.

Reeller Fall

Seien λ1\lambda_1 und λ2\lambda_2 die reellen Eigenwerte der Matrix A=(abcd)A=\pmatrix{ a & b \\ c & d} mit λ1≠λ2\lambda_1\neq \lambda_2. Wir wollen die Integrationskonstanten als positiv annehmen. Der Durchlaufsinn der Ortskurven hängt dann nur von den Vorzeichen von λ1\lambda_1 und λ2\lambda_2 ab.
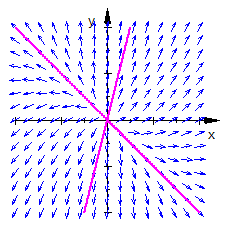
PlusPlus.png
Quelle für zwei positive Eigenwerte

Positive Eigenwerte

Es handelt sich um einen instabilen Knoten im Ursprung, eine Quelle.
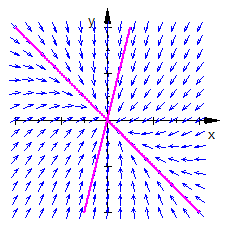
MinusMinus.png

Negative Eigenwerte

In diesem Fall ist der Knoten stabil. Es handelt sich um eine Senke, zu der die Kurven hinströmen.
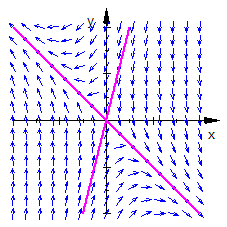
PlusMinus.png

Gemischte Eigenwerte

Während in einem Sektor zur Ursprung hingeströmt wird, strömt es im anderen Sektor weg. Es liegt ein Sattelpunkt (Wirbel) vor.

Komplexer Fall

Es liegen zwei konjugiert komplexe Eigenwerte der Form λ1=a+i⁡b\lambda_1=a+\i b und λ2=a−i⁡b\lambda_2=a-\i b vor.
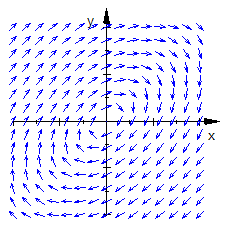
ReNu.png

Realteil a=0a=0

Die Ortskurven sind Ellipsen mit dem Zentrum im Ursprung.
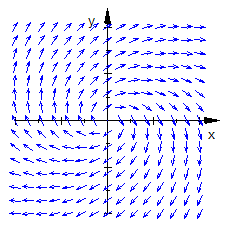
RePos.png

Realteil a>0a>0

Die Ortskurven sind Spiralen, die sich vom Ursprung weg bewegen.
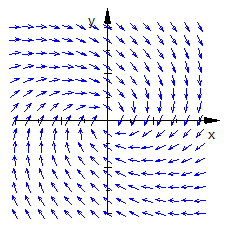
ReNeg.png

Realteil a<0a<0

Die Ortskurven sind Spiralen, die sich zum Ursprung hin bewegen.
 
 

Im großen Garten der Geometrie kann sich jeder nach seinem Geschmack einen Strauß pflücken.

David Hilbert

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Konstante Koeffizienten