Betragsungleichungen

Bei Betragsungleichungen handelt es sich um Ungleichungen, in denen Beträge vorkommen. Sie werden in der Regel durch Fallunterscheidung gelöst.

Beispiel

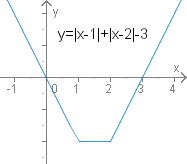
BetragsUgl.png
∣x−1∣+∣x−2∣≤3|x-1|+|x-2|\leq 3(1)

Grafische Lösung

Nebenstehende Grafik zeigt das Bild der Funktion f(x)=∣x−1∣+∣x−2∣−3f(x)=|x-1|+|x-2|- 3, die Lösungsmenge LL enthält alle Werte, für die der Graph unterhalb der x-Achse verläuft. Als grafische Lösung erhalten wir das Intervall L=[0,3]L=[0,3].
 
 

Rechnerische Lösung durch Fallunterscheidung

Kriterium für die gewählten Fälle bei der Lösung von (1) sind die Intervalle, in denen einzelne Teile des Terms das Vorzeichen wechseln.
Fall 1: x<1x<1
Es gilt x−1<0x-1<0 und x−2<0x-2<0 und (1) vereinfacht sich zu
−(x−1)+−(x−2)=−x+1−x+2=−2x+3≤3-(x-1)+-(x-2)=-x+1-x+2=-2x+3\leq 3,
was äquivalent zu −2x≤0-2x\leq0 und x≥0x\geq0 ist.
Damit haben wir die erste Teillösung gefunden: L1=[0,1[L_1=[0,1[.
Fall 2: 1≤x<21\leq x <2
In diesem Fall gilt x−1≥0x-1\geq 0 und x−2<0x-2<0 und (1) vereinfacht sich zu
x−1+−(x−2)=x−1−x+2=1≤3x-1+-(x-2)=x-1-x+2=1\leq 3,
was immer war ist. Also: L2=[1,2[L_2=[1,2[.
Fall 3: x≥2x\geq 2
Jetzt sind die beiden Terme positiv und es gilt:
x−1+x−2=2x−3≤3x-1+x-2=2x-3\leq3,
was äquivalent zu 2x≤62x\leq 6 und x≤3x\leq 3 ist. Damit ist L3=[2,3]L_3=[2,3].
Für die Lösungsmenge LL von (1) gilt:
L=L1∪L2∪L3=[0,1[∪[1,2[∪[2,3]=[0,3]L=L_1\cup L_2\cup L_3=[0,1[\cup[1,2[\cup[2,3]=[0,3],
was der grafischen Lösung entspricht.

Es gibt Dinge, die den meisten Menschen unglaublich erscheinen, die nicht Mathematik studiert haben.

Archimedes

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Reelle Zahlen