Affine Koordinatenebenen

Sei K\K ein beliebiger Körper und V=(K2,K)V=(\K^{2},\K) der kanonische zweidimensionale Vektorraum über K\K. Die Punkte seien die Elemente aus K2\K^{2} und die Geraden Teilmengen der Form
g(a,b)={a+tb ∣ a,b∈K2,t∈K,b≠0}g(\vec{a},\vec{b})=\{\vec{a}+t\vec{b}\verts\vec{a},\vec{b}\in\K^{2},t\in\K,\vec{b}\neq\vnull\}.(1)
Nach dieser Definition gilt a∈g(a,b)\vec{a}\in g(\vec{a},\vec{b}) (für t=0t=0) und a+b∈g(a,b)\vec{a}+\vec{b}\in g(\vec{a},\vec{b}) (für t=1t=1). Eine Struktur mit Punkten aus K2\K^2 und Geraden der Form (1) heißt Koordinatenebene.
Im weiteren werden wir jedoch eine Darstellung für Geraden bevorzugen, die an die Hessesche [1] Normalform angelehnt ist. Dazu definieren wir zuerst einen Normalenvektor.
 
 

Normalenvektoren

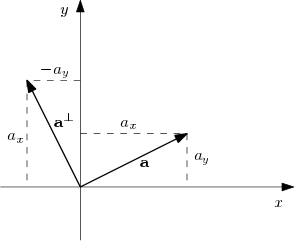
302_Ortho.png
Veranschaulichung des Normalenvektors
Im zweidimensionalen Vektorraum V=(K2,K)V=(\K^{2},\K) definieren wir zu einem Vektor a=(axay)\vec{a}=\evec{a_{x}}{a_{y}} den Normalenvektor a⊥=(−ayax)\voc a=\evec{-a_{y}}{a_{x}}. Anschaulich entspricht dies im R2\R^{2} einer Drehung um den Ursprung um 90°90° entgegen dem Uhrzeigersinn (vgl. Abb. ). Die Ursprungsgeraden durch a\vec{a} und a⊥\vec{a}\oc stehen senkrecht aufeinander. Das gewählte Symbol ⊥\oc soll dies andeuten.
Gleichwertige Resultate würden wir erzielen, hätten wir (ay−ax)\evec{a_{y}}{-a_{x}} als Normalenvektor gewählt. Wir haben uns jedoch für diese Definition entschieden, da sie einer Drehung in mathematisch positiven Drehsinn entspricht.

Satz UB20 (Eigenschaften der Normalenvektoren)

Seien a,bc∈K2\vec{a},\vec{b}\vec{c}\in\K^{2} und α,β,λ∈K\alpha,\beta,\lambda\in\K. Dann gilt:
  1. ⊥:K2→K2\oc:\K^{2}\to\K^{2} ist eine lineare Abbildung, also (αa+βb)⊥=αa⊥+βb⊥(\alpha\vec{a}+\beta\vec{b})\oc=\alpha\voc a+\beta\voc b
  2. a⊥⊥=−a{\vec{a}}\occ=-\vec{a}
  3. ⟨a⊥,b⟩=−⟨a,b⊥⟩\la{\voc a},{\vec{b}}\ra=-\la{\vec{a}},{\voc b}\ra, speziell ⟨a⊥,a⟩=⟨a,a⊥⟩=0\scprod{\voc a}{\vec{a}}=\la{\vec{a}},{\voc a}\ra=\vnull
  4. ⟨a,b⊥⟩=0\la{\vec{a}},{\voc b}\ra=0} gdw. es gibt ein 0≠λ∈K0\ne\lambda\in\K mit b=λa\vec{b}=\lambda\vec{a}, falls a,b≠0\vec{a},\vec{b}\ne\vnull
  5. ⟨a,b⊥⟩c+⟨b,c⊥⟩a+⟨c,a⊥⟩b=0\la\vec{a},\voc b\ra\vec{c}+\la\vec{b},\voc c\ra\vec{a}+\la\vec{c},\voc a\ra\vec{b}=\vnull
[!Punkt] (v) ist eine andere Formulierung für: je drei Vektoren sind linear abhängig. Wir können also mit Hilfe von Normalenvektoren auf einfache Weise eine Linearkombination für drei Vektoren ausdrücken.

Beweis

Der Beweis von (i) - (iii) und (v) ist durch einfaches Einsetzen der Definition und Ausrechnen zu führen und sei dem Leser überlassen.
(iv) Sei ⟨a,b⊥⟩=0\la{\vec{a}},{\voc b}\ra=0, dann gilt nach Definition axby=aybxa_{x}b_{y}=a_{y}b_{x}. Wir müssen zeigen, dass ein λ≠0\lambda\ne0 existiert mit bx=λaxb_{x}=\lambda a_{x} und by=λayb_{y}=\lambda a_{y}. Im Fall ax=0a_{x}=0 gilt 0=aybx0=a_{y}b_{x} und da wegen a≠0\vec{a}\ne\vnull nun ay≠0a_{y}\ne0 gilt, ist bx=0b_{x}=0. Da by≠0b_{y}\ne0 ist mit λ=byay\lambda=\frac{b_{y}}{a_{y}} die Behauptung erfüllt. Im Fall ax≠0a_{x}\ne0 gilt by=bxaxayb_{y}=\frac{b_{x}}{a_{x}}a_{y} und wir wählen λ=bxax\lambda=\frac{b_{x}}{a_{x}} und Behauptung ist erfüllt, da notwendigerweise bx≠0b_{x}\ne0.
Nun gelte b=λa\vec{b}=\lambda\vec{a} mit λ≠0\lambda\ne0, also ⟨a,b⊥⟩=⟨a,(λa)⊥⟩=λ⟨a,a⊥⟩=0\la{\vec{a}},{\voc b}\ra=\la{\vec{a}},{(\lambda\vec{a)}\oc}\ra=\lambda\scprod{\vec{a}}{\voc a}=0, wobei wir (iii) benutzt haben. □\qed
Wir führen nun eine weitere Geradendefinition ein. Für a,b∈K2\vec{a},\vec{b}\in\K^{2} wobei b≠0\vec{b}\ne\vnull sei die Gerade g^(a,b)\hat{g}(\vec{a},\vec{b}) definiert durch
g^(a,b)={x∈K2 ∣ ⟨x,b⊥⟩=⟨a,b⊥⟩}\hat{g}(\vec{a},\vec{b})=\{\vec{x}\in\K^{2}\verts\scprod{\vec{x}}{\voc b}=\scprod{\vec{a}}{\voc b}\}
Es gilt also für x∈K2:x∈g^(a,b)\vec{x}\in\K^{2}:\vec{x}\in\hat{g}(\vec{a},\vec{b})  ⟺  ⟨x,b⊥⟩=⟨a,b⊥⟩\iff\la{\vec{x}},{\voc b}\ra=\la{\vec{a}},{\voc b}\ra  ⟺  ⟨x−a,b⊥⟩=0\iff\la\vec{x}-\vec{a},\voc b\ra=0.
Da die rechte Seite eine Zahl aus K\K ist, handelt es sich bei dieser Definition faktisch um die Hessesche Normalform einer Geraden. Der Vorteil dieser Geradendefinition gegenüber der von (1) ist, dass sie ohne einen Parameter tt auskommt und nur mit den Vektoren aus K2\K^{2}, dem Skalarprodukt und dem Normalenvektor formuliert werden kann. Beide Definitionen sind jedoch gleichwertig.

Satz IU75

Sei g^(a,b)\hat{g}(\vec{a},\vec{b}) eine Gerade. Dann gilt g^(a,b)={a+λb ∣ λ∈K}\hat{g}(\vec{a},\vec{b})=\{\vec{a}+\lambda\vec{b}\verts\lambda\in\K\}. Speziell a∈g^(a,b)\vec{a}\in\hat{g}(\vec{a},\vec{b}) für λ=0\lambda=0 und a+b∈g^(a,b)\vec{a}+\vec{b}\in\hat{g}(\vec{a},\vec{b}) für λ=1\lambda=1. Damit ist g^(a,b)\hat{g}(\vec{a},\vec{b})=g(a,b)g(\vec{a},\vec{b}).

Beweis

Es gilt offensichtlich a∈g(a,b)\vec{a}\in{g}(\vec{a},\vec{b}) und a∈g^(a,b)\vec{a}\in\hat{g}(\vec{a},\vec{b}). Sei nun x≠a\vec{x}\ne\vec{a}. dann ergibt sich mit Satz UB20 (iv): x=a+tb\vec{x}=\vec{a}+t\vec{b} für ein t≠0t\neq0   ⟺  x−a=tb\iff\vec{x}-\vec{a}=t\vec{b}   ⟺  ⟨x−a,b⊥⟩=⟨tb,b⊥⟩=0\iff\scprod{\vec{x}-\vec{a}}{\voc b}=\scprod{t\vec{b}}{\voc b}=0   ⟺  ⟨x,b⊥⟩=⟨a,b⊥⟩\iff\scprod{\vec{x}}{\voc b}=\scprod{\vec{a}}{\voc b}   ⟺  x∈g^(a,b)\iff\vec{x}\in\hat{g}(\vec{a},\vec{b}). □\qed

Da nun g(a,b)=g^(a,b)g(\vec{a},\vec{b})=\hat{g}(\vec{a},\vec{b}) gilt und keine Verwechslungen zu befürchten sind, schreiben wir nun stets gg für g^\hat{g}.

Satz HT65

Jede Koordinatenebene ist eine Inzidenzebene. Dabei sind die Punkte die Elemente aus K2\K^{2} und die Geraden alle g(a,b)={x∈K2 ∣ ⟨x,b⊥⟩=⟨a,b⊥⟩}g(\vec{a},\vec{b})=\{\vec{x}\in\K^{2}\verts\scprod{\vec{x}}{\voc b}=\scprod{\vec{a}}{\voc b}\} für a,b∈K2\vec{a},\vec{b}\in\K^{2} mit b≠0\vec{b}\ne\vnull.

Beweis

Inz1: Seien a,b∈K2\vec{a},\vec{b}\in\K^{2} , wir zeigen, dass g(a,b−a)g(\vec{a},\vec{b}-\vec{a}) die von a\vec{a} und b\vec{b} eindeutig bestimmte Gerade ist. Nach Definition handelt es sich um eine Gerade. Nach Satz IU75 gilt a,b∈g(a,b−a)\vec{a},\vec{b}\in g(\vec{a},\vec{b}-\vec{a}). Bleibt nachzuweisen, dass g(a,b−a)g(\vec{a},\vec{b}-\vec{a}) eindeutig bestimmt ist. Angenommen g(c,d)g(\vec{c},\vec{d}) ist eine andere Gerade, die sowohl a\vec{a} als auch b\vec{b} enthält. Dann gilt zunächst ⟨a,d⊥⟩=⟨b,d⊥⟩=⟨c,d⊥⟩\la\vec{a},\voc d\ra=\la\vec{b},\voc d\ra=\la\vec{c},\voc d\ra und damit ⟨b−a,d⊥⟩=0\la\vec{b}-\vec{a},\voc d\ra=0 und nach Satz UB20 gibt es ein λ≠0\lambda\ne0, sodass b−a=λd\vec{b}-\vec{a}=\lambda\vec{d}. Sei nun x∈K2\vec{x}\in\K^{2} ein beliebiger Punkt auf der Geraden g(a,b−a)g(\vec{a},\vec{b}-\vec{a}). Dann gilt folgende Äquivalenzkette: x∈g(a,b−a)\vec{x}\in g(\vec{a},\vec{b}-\vec{a})   ⟺  ⟨x−a,(b−a)⊥⟩=0\iff\la\vec{x}-\vec{a},(\vec{b}-\vec{a})\oc\ra=0   ⟺  ⟨x−a,(λd)⊥⟩=0\iff\la\vec{x}-\vec{a},(\lambda\vec{d})\oc\ra=0   ⟺  ⟨x−a,d⊥⟩=0\iff\la\vec{x}-\vec{a},\voc d\ra=0   ⟺  ⟨x,d⊥⟩=⟨a,d⊥⟩=⟨c,d⊥⟩\iff\la\vec{x},\voc d\ra=\la\vec{}a,\voc d\ra=\la\vec{c},\voc d\ra   ⟺  x∈g(c,d)\iff\vec{x}\in g(\vec{c},\vec{d}). Daher gilt x∈g(a,b−a)=g(c,d)\vec{x}\in g(\vec{a},\vec{b}-\vec{a})=g(\vec{c},\vec{d}) und die die von a\vec{a} und b\vec{b} bestimmte Gerade ist eindeutig, womit Inz1 nachgewiesen wäre.
Inz2 ist trivial erfüllt und wir haben in Satz IU75 auch schon die zwei Punkte angegeben, die stets auf einer Geraden g(a,b)g(\vec{a},\vec{b}) liegen: a\vec{a} und a+b\vec{a}+\vec{b}.
Inz3: Sei nun a=(0,0)⊤\vec{a}=\evect00, b=(0,1)⊤\vec{b}=\evect01 und c=(1,0)⊤\vec{c}=\evect10. Dann sind diese drei Punkte verschieden, da in jedem Körper 0≠10\ne1 gilt. Wir zeigen dass sie auch nicht kollinear sind. Angenommen c∈g(a,b−a)\vec{c}\in g(\vec{a},\vec{b}-\vec{a}), dann gilt nach Satz IU75 für ein λ∈K\lambda\in\K: (1,0)⊤=(0,0)⊤+λ(0,1)⊤=t(0,1)⊤\evect10=\evect00+\lambda\evect01=t\evect01, also 1=λ⋅01=\lambda\cdot0, was für kein λ∈K\lambda\in\K erfüllt ist. Damit ist die Annahme, dass c\vec{c} auf der Geraden durch a\vec{a} und b\vec{b} liegt, widerlegt. □\qed
 
1  Otto Hesse 1811-1874

Es gibt jedoch noch einen anderen Grund für die hohe Wertschätzung der Mathematik; sie allein bietet den Naturwissenschaften ein gewisses Maß an Sicherheit, das ohne Mathematik nicht erreichbar wäre.

Albert Einstein

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Synthetische Geometrie