Beispiele affiner Koordinatenebenen
Beispiel CK37 (Minimale affine Koordinatenebene)
Wie sieht die kleinste affine Koordinatenebene aus? Sei der Galoiskörper mit zwei Elementen und , der kleinst mögliche Körper überhaupt. Wir betrachten den Vektorraum . Es gibt genau vier Punkte: , , und und die sechs Geraden sind dann , , , , und . Abb. 1 a) veranschaulicht diese affine Koordinatenebene; wobei sich die Geraden und natürlich nicht schneiden. Dies wird durch die Umordnung der Punkte in Abb. 1 b) deutlich. Diese Struktur ist isomorph zur minimalen affinen Ebene aus Beispiel UI60 gefunden. Nach ??? ist dies kein Zufall ist, denn jede affine Koordinatenebene ist eine affine Ebene.
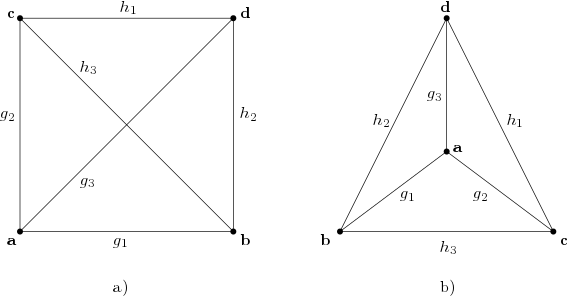
Abb. 1: Zwei Darstellungen der minimalen affinen Koordinatengeometrie mit . a) koordinatenorientiert, b) als Tetraeder.
Beispiel (Euklidische Ebene
Betrachten wir nun den Körper der komplexen Zahlen als Vektorraum über so erhalten wir eine zur euklidischen Ebene identische (=isomorphe) affine Ebene. Denn bis auf Isomorphie gibt es nur einen zweidimensionalen Vektorraum über .
Anders liegt der Fall beim Vektorraum . Dieser liefert ebenfalls eine affine Koordinatenebene, die sich jedoch von der euklidischen Ebene unterscheidet.
Das Buch der Natur ist mit mathematischen Symbolen geschrieben.
Galileo Galilei
Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf
ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld
• Dοrfplatz 25 • 17237 Blankеnsее
• Tel.: 01734332309 (Vodafone/D2) •
Email: cο@maτhepedιa.dе