Beispiele für Inzidenzebenen
Das Aufstellen von Axiomen sagt noch nichts über die Existenz der Objekte aus, für die die Axiome gelten sollen. Um sich hier nicht "festzufahren" ist es am besten ein Modell anzugeben, das die Axiome erfüllt. Dies wird in den folgenden Beispiel geschehen, womit wir dann auch gleichzeitig nachweisen, dass das Axiomensystem nicht "inhaltsleer" ist.
Die Anschauungsebene erfüllt alle drei Inzidenzaxiome und ist damit ein Beispiel einer Inzidenzebene mit unendlich vielen Punkten und Geraden. Eine Inzidenzstruktur muss nicht notwendig unendlich viele Punkte enthalten. Inz3 fordert aber, dass es mindestens drei Punkte gibt.
Bei der Darstellung endlicher Inzidenzstrukturen zeichnen wir die die Punkte in der Anschauungsebene. Sie werden durch Strecken oder allgemeine Kurven verbunden, um die Geraden anzudeuten. Die Geraden gehen ausschließlich durch die hervorgehobenen Punkte. Sollte es weitere Schnittpunkte in der Anschauungsebene geben, so sind diese normalerweise keine Punkte unserer Inzidenzstrukturen, es sei denn sie sind als solche gekennzeichnet.
Beispiel AV45 (Zweielementige Teilmengen als Geraden)
Wir können zu jeder endlichen Menge (mit mindestens drei Elementen) eine Inzidenzstruktur konstruieren. Sei eine beliebige Menge mit . Diese Elemente seien unsere Punkte. Wir wählen als Geraden die Menge aller zweielementigen Teilmengen von . Es ist Inz1 erfüllt, da es für je zwei Elemente aus genau eine zweielementige Teilmenge gibt. Und nach Definition enthält auch jede Gerade mindestens zwei Punkte, womit Inz2 erfüllt ist. Seien nun drei beliege verschiedene Punkte, dann können diese nicht auf einer Geraden liegen, da ja unsere Geraden genau die zweielementigen Teilmengen von waren, damit sind sogar alle Punktetripel in allgemeiner Lage.
Beispiel AJ15 (Minimale Inzidenzebene)
Konkretisieren wir die Überlegungen aus dem vorherigen Beispiel für drei Punkte, so bekommen wir die minimale Inzidenzebene. Seien , und unsere Punkte, dann erhalten wir die folgenden Geraden , und . Abb. 1 a) veranschaulicht diese Inzidenzebene. Nach obigen Überlegungen sind alle drei Inzidenzaxiome erfüllt, damit ist dieses System tatsächlich ein Modell für eine Inzidenzebene.
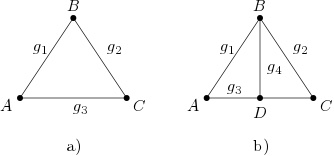
Abb. 1 a) minimale Inzidenzebene mit drei Punkten und drei Geraden, b) Inzidenzebene, bei der es eine Gerade mit mehr als zwei Punkten gibt.
Wir können der Gerade einen weiteren Punkt hinzufügen und eine weitere Gerade hinzunehmen und erhalten so eine Inzidenzgeometrie, die eine Gerade mit drei Punkten enthält, wie in Abb. 1 b) argestellt. Die Inzidenzaxiome sind nach wie vor erfüllt.
Nach unserer bisherigen Erfahrung sind wir zum Vertrauen berechtigt, dass die Natur die Realisierung des mathematisch denkbar Einfachsten ist.
Albert Einstein
Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf
ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld
• Dοrfplatz 25 • 17237 Blankеnsее
• Tel.: 01734332309 (Vodafone/D2) •
Email: cο@maτhepedιa.dе