Weitere Sätze über Inzidenzebenen

Zunächst charakterisieren wir die Gleichheit von Verbindungsgeraden.

Satz WI24

Für drei verschiedene Punkte A,B,CA,B,C einer Inzidenzebene sind die folgenden beiden Aussagen äquivalent
  1. CC liegt auf der Geraden durch AA und BB: C∈A ⊻ BC\in A\vgr B.
  2. Die Verbindungsgeraden von AA und BB und von AA und CC sind gleich: A ⊻ B=A ⊻ CA\vgr B=A\vgr C.

Beweis

(i)   ⟹  \implies (ii): Sei C∈A ⊻ B=gC\in A\vgr B=g, dann geht die Gerade gg durch AA und CC und mit Inz1 gilt: g=A ⊻ B=A ⊻ Cg=A\vgr B=A\vgr C. (ii)   ⟹  \implies (i): Aus A ⊻ B=A ⊻ CA\vgr B=A\vgr C folgt C∈A ⊻ C=A ⊻ BC\in A\vgr C=A\vgr B, also gilt (i). □\qed

Geraden können auch keinen echten "Teilgeraden" enthalten, denn es gilt:
 
 

Satz NF12

Seien gg und hh zwei Geraden einer Inzidenzebene. Dann folgt aus g⊆hg\subseteq h bereits g=hg=h. Für zwei verschiedene Geraden gg und hh gibt es also stets einen Punkt, der auf der einen, aber nicht auf der anderen Geraden liegt.

Beweis

Seien nach Inz2 AA und BB zwei verschiedene Punkte der Geraden gg, dann liegen diese auch auf hh und es gilt mit Inz1 g=A ⊻ B=hg=A\vgr B=h. □\qed

Satz CB36

In jeder Inzidenzebene gilt:
  1. Für jede Gerade gibt es einen Punkt, der nicht auf dieser Geraden liegt.
  2. Für jeden Punkt gibt es eine Gerade, die nicht durch diesen Punkt geht.

Beweis

(i): Angenommen (i) gilt nicht, dann muss es eine Gerade geben, die alle Punkte enthält. Damit gibt es im Widerspruch zu Inz3 aber keine drei Punkte in allgemeiner Lage.
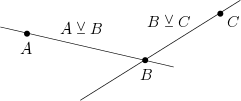
(ii): Zur Veranschaulichung verfolge man die Beweisschritte in Abb. 1.
Zupugr.png
Abb. 1: Zum Beweis von Satz CB36 (ii). Punkt AA liegt nicht auf der Geraden durch die Punkte BB und CC
Sei AA ein Punkt, dann gibt es nach Inz3 einen weiteren von AA verschiedenen Punkt BB und nach Inz1 die eindeutig von ihnen bestimmte Verbindungsgerade A ⊻ BA\vgr B. Nach (i) gibt es dann einen Punkt CC, der nicht auf A ⊻ BA\vgr B liegt. Das bedeutet aber nach Satz WI24, dass A ⊻ BA\vgr B und die Verbindungsgerade B ⊻ CB\vgr C verschieden sind. Wegen Satz F1UF liegt damit AA dann aber nicht auf B ⊻ CB\vgr C, womit wir eine Gerade gefunden haben, die AA nicht enthält. □\qed
Damit haben wir in Inzidenzgeometrien eine gewisse Vielfalt. Es liegen nicht alle Punkte auf einer Geraden und nicht alle Geraden gehen durch einen Punkt.

Satz NM69 (Unabhängigkeit der Inzidenzaxiome)

Die drei Inzidenzaxiome Inz1-Inz3 sind voneinander unabhängig.

Beweis

Wir beweisen dies, indem wir ein Beispiel für eine Struktur angeben, die jeweils zwei der Axiome erfüllt, das dritte jedoch nicht.
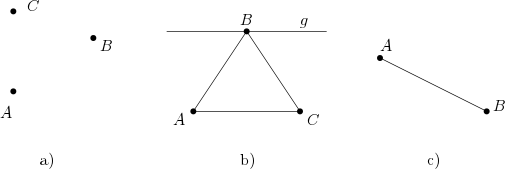
UnabhInz.png
Abb. 2: Unabhänigkeit der Inzidenzaxiome a) Inz1 verletzt, b) Inz2 verletzt, c) Inz3 verletzt
Die isolierten drei Punkte aus Abb. 2 a) liefern ein Beispiel, wo Inz1 nicht erfüllt ist, jedoch die beiden anderen Axiome.
Abb. 2 b) zeigt ein Beispiel, wo Inz2 verletzt ist. Auf der Geraden gg liegt nur der eine Punkt BB.
Abb. 2 c) zeigt ein Beispiel, wo Inz3 verletzt ist, da es nur die beiden Punkte AA und BB gibt.
Die beiden anderen Axiome sind in allen Beispielen jeweils erfüllt, wovon man sich leicht überzeugt, da es sich um endliche Strukturen mit wenigen Punkten handelt. □\qed

Seit die Mathematiker über die Relativitätstheorie hergefallen sind, verstehe ich sie selbst nicht mehr.

Albert Einstein

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Synthetische Geometrie