Projektive Ebenen
Wie sieht eine Geometrie ohne parallele Geraden aus? Um dies zu untersuchen verwenden wir die folgenden Axiome: Inz4
Inz5
Eine Struktur, die den Axiomen Inz1 bis Inz5 genügt heißt projektive Ebene.
Auf Inz2 können wir verzichten, da Inz5 es umfasst. Wegen Satz WH94 genügt für Inz4 die schwächere Formulierung, dass sich verschiedene Geraden in mindestens einem Punkt schneiden.
Satz PW94
Jede projektive Ebene ist eine Inzidenzebene.
Die Umkehrung muss natürlich nicht gelten, wie die minimale Inzidenzebene aus Beispiel AJ15 zeigt, bei der auf jeder Gerade nur zwei Punkte liegen. Natürlich ist eine affine Ebenen keine projektive Ebene, da nach Axiome Inz4 keine Parallelen existieren.
Die Umkehrung muss natürlich nicht gelten, wie die minimale Inzidenzebene aus Beispiel AJ15 zeigt, bei der auf jeder Gerade nur zwei Punkte liegen. Natürlich ist eine affine Ebenen keine projektive Ebene, da nach Axiome Inz4 keine Parallelen existieren.
Satz ME69
Beweis
Zum Beweis von Satz ME69
Nach Satz QQ23 bleibt lediglich der Fall auszuschließen, dass durch einen Punkt genau zwei Geraden gehen. Angenommen, der Punkt liegt genau auf zwei Geraden und . Dann gibt es nach Inz5 auf jeder dieser Geraden mindestens einen weiteren Punkt bzw. . liegt nicht auf der Verbindungsgerade , da sonst nach Satz WI24 die Geraden und gleich wären, im Widerspruch dazu, dass durch zwei verschiedene Geraden gehen. Nach Axiom Inz5 enthält die Gerade einen weiteren Punkt , der von und verschieden ist. Nach Inz1 existiert die Verbindungsgerade , diese kann aber weder mit noch mit identisch sein. Damit gibt es eine dritte Gerade durch den Punkt , im Widerspruch zur Annahme, dass durch genau zwei Geraden gehen.
Satz ME69 erlaubt es ein Dualitätsprinzip für projektive Ebenen aufzustellen. Tauschen wir nämlich die Begriffe Punkte mit Geraden und "Punkt liegt auf Gerade" mit "Gerade enthält Punkt", dann erhalten wir wieder eine projektive Ebene, nämlich die duale Ebene.
Satz ME69 erlaubt es ein Dualitätsprinzip für projektive Ebenen aufzustellen. Tauschen wir nämlich die Begriffe Punkte mit Geraden und "Punkt liegt auf Gerade" mit "Gerade enthält Punkt", dann erhalten wir wieder eine projektive Ebene, nämlich die duale Ebene.
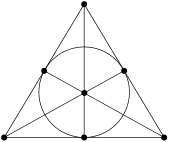
Beispiel (Fano-Ebene)
Inz5 fordert, dass alle Geraden mindestens drei Punkte enthalten und nach Satz ME69 wissen wir, dass durch jede Gerade mindestens drei Punkte gehen. In der in Abb. IP96 veranschaulichten projektiven Ebene hat jede Gerade genau drei Punkte und durch jeden Punkt gehen genau drei Geraden. Sie heißt Fano-Ebene[1].
Beispiel
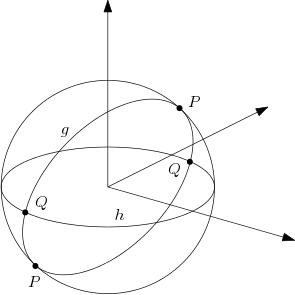
Wir betrachten als Punkte alle Punkte auf der Oberfläche der Einheitskugel. Die Geraden seien die Großkreise. Dann sind die Axiome Inz2 und Inz3 und sogar Inz5 erfüllt, jedoch Inz1 nicht, denn für zwei diametral gegenüberliegende Punkte gibt es unendlich viele Großkreise, die diese Punkte enthalten.
Identifizieren wir wie in Abb. AK83 angedeutet diese diametral gegenüberliegenden Punkte und definieren diese Paare als Punkte, ist nun auch Inz1 erfüllt. Die "Gerade" ist z.B. genau der Großkreis durch die Punkte und . Die Geraden und schneiden sich im Punkt . Damit handelt es sich nicht nur um eine Inzidenzstruktur, sondern sogar um eine projektive Ebene.
Satz PK75
In einer projektiven Ebene gibt es wenigstens vier verschiedene Punkte, von denen jeweils drei nicht kollinear sind. Es existieren also echte Vierecke.
Man kann die Axiomatik der projektivem Ebene auch basierend auf diesem Satz und den Axiomen Inz1 und Inz4 aufbauen. Der von uns gewählte Weg erscheint uns jedoch besser zu sein, da die gewählten Axiome anschaulicher sind.
Man kann die Axiomatik der projektivem Ebene auch basierend auf diesem Satz und den Axiomen Inz1 und Inz4 aufbauen. Der von uns gewählte Weg erscheint uns jedoch besser zu sein, da die gewählten Axiome anschaulicher sind.
Beweis
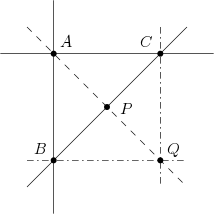
Abb. TU01: Zum Beweis von Satz PK75
Wir werden die vier gesuchten Punkte konstruieren und zeigen, dass sie die geforderten Eigenschaften haben, dabei mag dem Leser Abb. TU01 beim Nachvollziehen der Beweisschritte helfen. Wir benutzen häufig Satz WI24 ohne darauf explizit hinzuweisen.
Wir gehen von drei nicht kollinearen Punkten , und aus, deren Existenz nach Inz3 gesichert ist. Auf der Verbindungsgeraden liegt nun nach Inz5 ein weiterer Punkt . Es gilt außerdem , denn andererseits wäre , also , im Widerspruch dass , und nicht kollinear sind. Weiterhin liegt weder auf noch auf . Denn mit und wäre der eindeutig bestimmte Schnittpunkt der beiden Verbindungsgeraden. Für argumentiert man analog.
Die Verbindungsgerade enthält wegen Inz5 auch noch einen dritten Punkt . Wir zeigen zunächst, dass dieser nicht mit oder übereinstimmen kann, daher also alle fünf von uns konstruierten Punkte verschieden sind, insbesondere dann auch ,, und verschiedene Punkte sind. Angenommen , dann wäre wegen nun sicher , dies hatten wir jedoch oben widerlegt. Man argumentiert wieder analog für .
Bleibt nur noch zu zeigen, dass für die vier Punkte ,, und jedes Tripel nicht auf einer Geraden liegt. Für , und ist dies klar, da sie genauso gewählt waren.
Wäre , dann wäre auch , also , was wir oben widerlegt haben. Die drei Punkte , und sind nicht kollinear.
Wäre , dann wäre auch , also , was wir oben widerlegt haben. Die drei Punkte , und sind nicht kollinear.
Wäre , dann wäre Sowohl als auch wären der eindeutige Schnittpunkt von , und damit im Widerspruch zu oben. Die drei Punkte , und sind nicht kollinear.
Inz2 ist eine schwächere Formulierung von Inz5, daher können die Axiome Inz1 bis Inz5 nicht unabhängig sein. Es gilt jedoch:
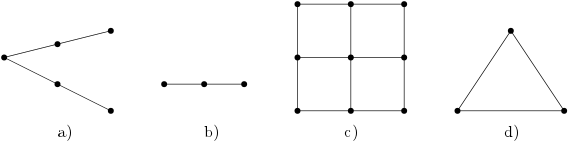
Satz XZ49 (Unabhängigkeit der Axiome der projektiven Ebene)
Beweis
In Abb. NE34 haben wir Beispiele für Strukturen angegeben, die jeweils ein Axiom erfüllen und die anderen drei verletzen.
Insbesondere gibt es in Abb. NE34 b) keine drei Punkte in allgemeiner Lage, zwei Geraden schneiden sich aber in einem Punkt, denn dies gilt trivial, da es nur eine Gerade gibt.
In Abb. NE34 c) gibt es parallele Geraden. Es handelt sich hier um eine affine Ebene. Jede affine Ebene mit Geraden mit wenigstens drei Punkten kann hier als Beispiel angeführt werden, also auch die euklidische Anschauungsebene.
Das Axiom Inz5 können wir durch eine schwächere Version ersetzen. Es reicht schon aus, wenn es zwei Geraden mit drei Punkten gibt:
Satz AY86
Gelten die Axiome Inz1, Inz3, Inz4 und gibt es zwei verschiedene Geraden mit mindestens drei Punkten, dann handelt es sich um eine projektive Ebene.
Beweis
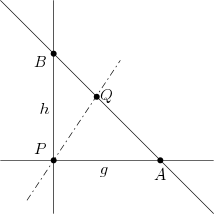
Seien und die zwei Geraden mit mindestens drei Punkten, dann zeigen wir, dass eine beliebige Gerade (,) ebenfalls mindestens drei Punkte enthält. Nach Inz4 existiert der Schnittpunkt . Die beiden folgenden Fälle sind in Abb. NA26 veranschaulicht.
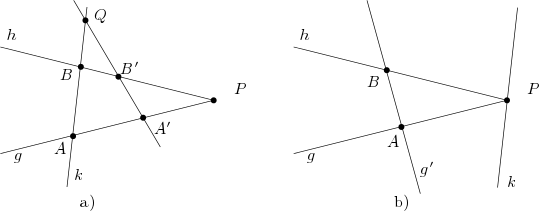
Abb. NA26: Zum Beweis von Satz AY86, a) Fall 1: , b) Fall 2:
Fall 1: liegt nicht auf . Seien und die Schnittpunkte mit der Geraden , welchen nach Inz4 existieren und auch verschieden sind. Wegen der Voraussetzung existieren auf und jeweils ein weiterer Punkt bzw. . Ihre Verbindungsgerade existiert nach Inz1 und ist sicher von verschieden. Sei nun der Schnittpunkt dieser Verbindungsgeraden mit . Damit sind , und drei verschiedene Punkte auf der Geraden .
Fall 2: liegt auf . Seien nun bzw. von verschiedene Punkte, die auf bzw. liegen und die Verbindungsgerade von und . Da nicht durch geht, können wir Fall 1 anwenden und so zeigen, dass mindestens drei Punkte enthält. Nun liegen , und wie im Fall 1, wobei die Rolle von übernimmt, da nicht durch geht, können wir Fall 1 tatsächlich anwenden und so zeigen, dass auf mindestens drei Punkte liegen.
1 Gino Fano 1871-1952, italienischer Mathematiker
Scherzhafte Beispiele haben manchmal größere Bedeutung als ernste.
Michael Stifel
Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf
ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld
• Dοrfplatz 25 • 17237 Blankеnsее
• Tel.: 01734332309 (Vodafone/D2) •
Email: cο@maτhepedιa.dе