Orthogonalität und Norm

In einem euklidischen Vektorraum kann die Orthogonalität zweier Vektoren allein durch die Norm charakterisiert werden. Es gilt

Satz 15WN (Orthogonalität und Norm)

Sei VV ein euklidischer Vektorraum mit dem Skalarprodukt ⟨⋅,⋅⟩\spo\cdot,\cdot\spc und der daraus induzierten Norm ∣∣⋅∣∣||\cdot||. Dann gilt für alle a,b∈Va,b\in V:
a⊥b  ⟺  ∣∣a+b∣∣=∣∣a−b∣∣a\perp b\iff ||a+b||=||a-b||

Beweis

Es gilt: ∣∣a+b∣∣=∣∣a−b∣∣||a+b||=||a-b||   ⟺  ⟨a+b,a+b⟩=⟨a−b,a−b⟩\iff \sqrt{\spo a+b,a+b\spc}=\sqrt{\spo a-b,a-b\spc}   ⟺  ⟨a+b,a+b⟩=⟨a−b,a−b⟩\iff {\spo a+b,a+b\spc}={\spo a-b,a-b\spc}   ⟺  ⟨a,a⟩+2⟨a,b⟩+⟨b,b⟩=⟨a,a⟩−2⟨a,b⟩+⟨b,b⟩\iff\spo a,a\spc+2\spo a,b\spc+\spo b,b\spc=\spo a,a\spc-2\spo a,b\spc+\spo b,b\spc   ⟺  2⟨a,b⟩=−2⟨a,b⟩\iff2\spo a,b\spc=-2\spo a,b\spc   ⟺  4⟨a,b⟩=0  ⟺  a⊥b\iff4\spo a,b\spc=0\iff a\perp b □\qed

Folgerung

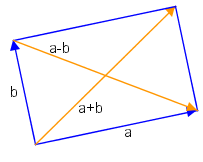
ReDiag.png
Ein Parallelogramm ist genau dann ein Rechteck, wenn seine Diagonalen gleich lang sind.
Man kann die Vektoren aa und bb als Seiten eines Vierecks auffassen, dann sind a+ba+b und a−ba-b aber genau die Diagonalen.
 
 

Im großen Garten der Geometrie kann sich jeder nach seinem Geschmack einen Strauß pflücken.

David Hilbert

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Euklidische Vektorräume