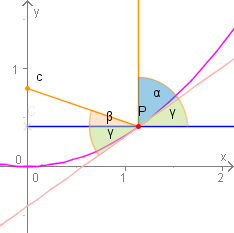
Differentialgleichung des Hohlspiegels

Wir wollen die Funktionsgleichung für einen Hohlspiegel herleiten. Die senkrecht auftreffenden Strahlen sollen dabei im Punkt (0;c)(0;c) gebündelt werden.

Herleitung der DGL

Spiegel.png
Aus der Grafik leiten wir folgende Beziehungen für einen Punkt P(x,y)P(x,y) auf der Kurve ab.
Die mit γ\gamma bezeichneten Winkel sind Scheitelwinkel und daher gleich.
α=90°−γ\alpha=90°-\gamma
β+γ=α\beta+\gamma=\alpha (Eintrittswinkel = Austrittswinkel)
  ⟹  β+γ=90°−γ\implies \beta+\gamma=90°-\gamma   ⟹  β=90°−2γ\implies \beta=90°-2\gamma
Es ist y′=tan⁡γy'=\tan\gamma und tan⁡β=c−yx\tan \beta=\dfrac {c-y} x.
c−yx=tan⁡β=tan⁡(90°−2γ)\dfrac {c-y} x=\tan \beta=\tan(90°-2\gamma) =cot⁡2γ=1tan⁡2γ=\cot 2\gamma=\dfrac 1 {\tan 2\gamma} (Satz 5220C)
tan⁡2γ=2tan⁡γ1−tan⁡2γ\tan 2\gamma=\dfrac {2\tan \gamma}{1-\tan^2\gamma} (Satz 160W)
  ⟹  c−yx=1−tan⁡2γ2tan⁡γ\implies \dfrac {c-y} x=\dfrac {1-\tan^2\gamma}{2\tan \gamma} =1−y′22y′=\dfrac {1-y'^2}{2y'}
Differentialgleichung des Hohlspiegels:
2y′(y−c)=x(y′2−1)2y'(y-c)=x(y'^2-1)

Lösung der DGL mittels Potenzreihenansatz

y=a0+a1x+a2x2+a3x3+…y=a_0+a_1x+a_2x^2+a_3x^3+\dots
Wir nehmen an, dass die Kurve durch den Ursprung geht, dann ist a0=0a_0=0.
y=a1x+a2x2+a3x3+…y=a_1x+a_2x^2+a_3x^3+\dots
y′=a1+2a2x+3a3x2+…y'=a_1+2a_2x+3a_3x^2+\dots
y′2=a12+4a1a2x+…y'^2=a_1^2+4a_1a_2x+\dots
Linke Seite: 2y′(y−c)=2(a1+2a2x+3a3x2+… )⋅2y'(y-c)=2(a_1+2a_2x+3a_3x^2+\dots)\cdot (−c+a1x+a2x2+a3x3+… )(-c+a_1x+a_2x^2+a_3x^3+\dots) =−2ca1+2a12x+…=-2ca_1+2a_1^2x+\dots
Rechte Seite: x(y′2−1)=x(a12−1+4a1a2x+… )x(y'^2-1)=x(a_1^2-1+4a_1a_2x+\dots) =(a12−1)x+…=(a_1^2-1)x+\dots
Kein Absolutglied auf der rechten Seite, also −2ca1=0-2ca_1=0   ⟹  \implies a1=0a_1=0
Die linke Seite vereinfacht sich zu:
2y′(y−c)=2(2a2x+3a3x2+… )⋅2y'(y-c)=2(2a_2x+3a_3x^2+\dots)\cdot (−c+a2x2+a3x3+… )(-c+a_2x^2+a_3x^3+\dots) =−4a2cx+…=-4a_2cx+\dots
und wegen
y′2=(2a2x+3a3x2+… )2=4a22x2+…y'^2=(2a_2x+3a_3x^2+\dots)^2=4a_2^2x^2+\dots
ist die rechte Seite:
x(y′2−1)=x(−1+4a22x2+… )x(y'^2-1)=x(-1+4a_2^2x^2+\dots) =−x+4a22x3+…=-x+4a_2^2x^3+\dots,
woraus sich a2=14ca_2=\dfrac 1 {4c} ergibt.
Auf der rechte Seite findet sich kein Ausdruck für x2x^2, damit ist a3=0a_3=0.
Rechnet man weitere Glieder aus, so zeigt sich, dass diese identisch verschwinden. Daher vermuten wir, dass die Parabel
y=14cx2y=\dfrac 1 {4c}x^2
die Lösung ist.
Einsetzen ergibt: y′=x2cy'=\dfrac x {2c}; y′2=x24c2y'^2=\dfrac {x^2} {4c^2} und 2y′(y−c)−x(y′2−1)2y'(y-c)-x(y'^2-1) =xc(x24c−c)−x(x24c2−1)=0=\dfrac x {c}\left(\dfrac {x^2} {4c}-c\right)-x\left(\dfrac {x^2} {4c^2}-1\right)=0
Daher ist der Name Parabolspiegel für einen Hohlspiegel durchaus berechtigt.
 
 

Die Mathematik muß man schon deswegen studieren, weil sie die Gedanken ordnet.

M. W. Lomonossow

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Spezielle Lösungsmethoden