Beispiel zur Lösung von DGL mittels Potenzreihen

Bei komplizierten Differentialgleichungen empfiehlt es sich bei der Methode der Potenzreihen, Schritt für Schritt vorzugehen und die errechneten Koeffizienten sofort wieder einzusetzen.

Das Anfangswertproblem $y(y'+x)=1$ mit $y(0)=1$, soll mittels Potenzreihe für $x_0=0$ gelöst werden.

Der Ansatz $y=a_0+a_1x+a_2x^2+a_3x^3+\dots$

ergibt wegen $y(0)=1$ sofort $a_0=1$.

$y'=a_1+2a_2x+3a_3x^2+\dots$

$y'+x=a_1+(2a_2+1)x+3a_3x^2+\dots$

Wir erhalten $a_0a_1=1$, voraus sich $a_1=1$ ergibt. Für die Vereinfachung der weiteren Rechnung schreiben wir die Reihen mit den bisherigen Ergebnissen auf und erhalten:

$y=1+x+a_2x^2+a_3x^3+\dots$

$y'+x=1+(2a_2+1)x+3a_3x^2+\dots$

Koeffizientenvergleich für $x$ führt auf $2a_2+1+1=0$ $\implies$ $a_2=-1$

$y=1+x-x^2+a_3x^3+\dots$

$y'+x=1-x+3a_3x^2+\dots$

Koeffizientenvergleich für $x^2$: $3a_3-1-1=0$ $\implies a_3=\dfrac 2 3$.

Damit ergibt sich die Näherungslösung $y(x)=1+x-x^2+\dfrac 2 3x^3$

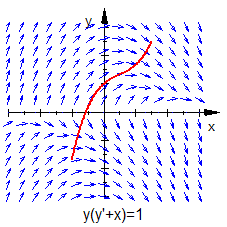
Vergleichen wir nun diese Näherungslösung (rote Linie in der Grafik) mit dem Richtungsfeld der DGL, sehen wir, dass dieses in der Nähe von $x=0$ sehr gut approximiert wird, für $|x|>\dfrac 1 2$ bricht der Graph jedoch schnell aus dem Richtungsfeld aus.