Schwerelinien und Schwerpunkt geometrischer Figuren

Sei FF eine Figur mit dem Flächeninhalt AA, eine Schwerelinie ist eine Gerade gg, die FF so teilt, dass jeweils die Hälfte der Figur in den beiden durch gg gebildeten Halbebenen liegt, dh die in den Halbebenen liegenden Teilfiguren haben jeweils den Flächeninhalt A/2A/2.
Der Schnittpunkt zweier Schwerelinien heißt Schwerpunkt. Wir werden sehen, dass sich 2 beliebige Schwerelinien stets in einem Punkt schneiden, sodass diese Definition gerechtfertigt ist.
 
 

Lemma C93A (Eigenschaften von Schwerelinien)

  1. Schneiden sich 2 Schwerelinien so sind dem Schnittpunkt gegenüberliegende Flächen gleich groß.
  2. Zwei verschiedene Schwerelinien besitzen stets einen gemeinsamen Schnittpunkt, können also nicht parallel sein.

Beweis

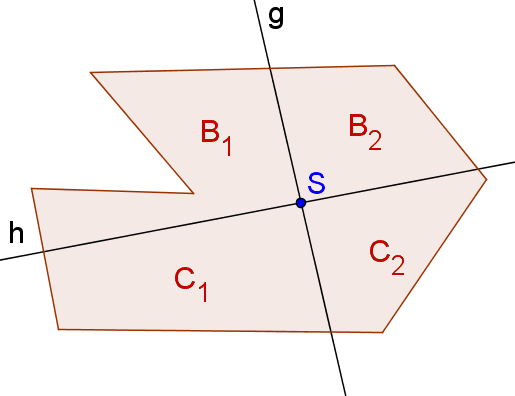
Sp.png
i) Seien gg und hh zwei sich schneidende Schwerelinien und AA der Flächeninhalt der Figur. Dann gilt (siehe nebenstehende [!Abbildung]): B1+B2=C1+C2=A2B_1+B_2=C_1+C_2=\dfrac A 2 und B1+C1=B2+C2=A2B_1+C_1=B_2+C_2=\dfrac A 2. Durch Subtraktion der Gleichungen können wir B2−C1=0B_2-C_1=0 und damit B2=C1B_2=C_1, ebenso B1−C2=0B_1-C_2=0 und damit B1=C2B_1=C_2.
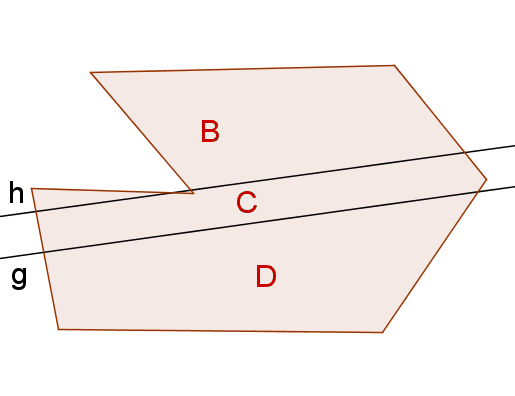
Sppa.png
ii) Seien gg und hh zwei parallele (aber verschiedene) Schwerelinien. Dann gilt für die Flächeninhalte (siehe nebenstehende [!Abbildung]): B+C=DB+C=D und B=C+DB=C+D, also 2⋅C=02\cdot C=0, die Parallelen müssen zusammenfallen. Widerspruch! □\qed

Satz C93B (Eindeutigkeit des Schnittpunktes von Schwerelinien)

Alle Schwerelinien einer Figur schneiden sich in einem eindeutig bestimmten Punkt, dem Schwerpunkt.

Beweis

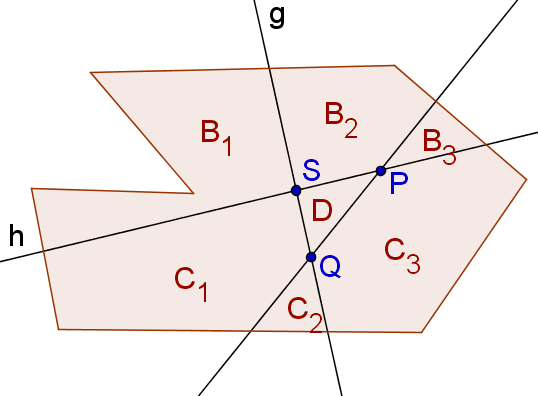
Sp3.png
Angenommen 3 verschiedene Schwerelinien schneiden sich nicht in einem Punkt, dann müssen sie - da je 2 von ihnen nach Lemma C93A nicht parallel sein können - ein Dreieck bilden. Wegen obigen Lemma gelten mit den Bezeichnungen in nebenstehender [!Abbildung] die folgenden Gleichungen:
B1=C3+DB_1=C_3+D, B2=C2+DB_2=C_2+D und B3=C1+DB_3=C_1+D.
Aufsummieren ergibt dies:
B1+B2+B3=C1+C2+C3+D+2DB_1+B_2+B_3=C_1+C_2+C_3+D+2D,
und da hh eine Schwerelinie ist: B1+B2+B3=C1+C2+C3+DB_1+B_2+B_3=C_1+C_2+C_3+D, also 2D=02D=0, damit müssen die Punkte PP, QQ und SS in einem Punkt zusammenfallen und sich die drei Schwerelinien in einem Punkt schneiden. □\qed

Alle Pädagogen sind sich darin einig: man muß vor allem tüchtig Mathematik treiben, weil ihre Kenntnis fürs Leben größten direkten Nutzen gewährt.

Felix Klein

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Abstrakte Radien zur Beschreibung ebener Figuren