MiMa-Sortierungen

Sei $P=\{p_1,\dots ,p_n\}$ ein endliches Poset. Dann können wir seine Elemente als Vektor $(p_1,\dots ,p_n)$ schreiben. Damit werden die Elemente von $P$ sortiert. Ist so ein Vektor gegeben sprechen wir auch von einer Sortierung. $(|\Mi(p_1)|,\dots ,|\Mi(p_n|)$ nennen wir den Mi-Vektor der Sortierung und $(|\Ma(p_1)|,\dots ,|\Ma(p_n|)$ ihren Ma-Vektor.

Gilt für eine Sortierung $k\le l \iff \my(p_k)\le \my(p_l)$, so nennen wir sie Mi-Sortierung. Ihr Vektor bildet eine monoton wachsende endliche Folge von natürlichen Zahlen. Analog nennen wir $(p_1,\dots ,p_n)$ Ma-sortiert, falls $k\le l \iff -\ny(p_k)\le -\ny(p_l)$. Der Ma-Vektor ist dementsprechend eine monoton fallende Folge natürlicher Zahlen. Da $\my$ und $\ny$ nicht injektiv sein muss, ist diese Soritierung nicht eindeutig bestimmt.

Seien $p_1,\dots ,p_n\in P$ die Elemente eines endlichen Poset Mi-sortiert oder Ma-sortiert. Dann ist die Ordnungsmatrix eine obere Diagonalmatrix.

Zu zeigen ist: für $i>j$ gilt $m_{ij}=0$. Angenommen $m_{ij}=1$, dann gilt $p_i\le p_j$, also $\Mi(p_i)\subseteq \Mi(p_j)$. Wegen $j\le i$ und da $P$ Mi-sortiert ist, gilt: $|\Mi(p_j)|\le |\Mi(p_i)|$. Damit kann $\Mi(p_i)$ keine echte Teilmenge von $\Mi(p_j)$ sein und es gilt $\Mi(p_i)=\Mi(p_j)$. Damit gilt $p_i,p_j\in Mi(p_i)=\Mi(p_j)$, also $p_i\le p_j\le p_i$, damit $p_i=p_j$ im Widerspruch zu $i\ne j$. Für die Ma-Sortierung führt man den Beweis analog. $\qed$

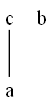
Nun stellt sich die Frage, ob eine Mi-Sortierung auch ein Ma-Sortierung ist. Im nebenstehende Hassediagramm ist die Sortierung $(a,b,c)$ eine Mi-Sortierung mit dem Mi-Vektor $(1,1,2)$ und auch eine Ma-Sortierung (Ma-Vektor: $(2,1,1)$). Tauschen wird die Positionen von $a$ und $b$, bleibt die Mi-Sortierung erhalten, die Ma-Sortierung ist aber nicht mehr gegeben.

Unter allen Mi-Sortierung finden wir wenigstens eine, die gleichzeitig eine Ma-Sortierung ist.

Wir nennen $p_1,\dots ,p_n\in P$ MiMa-sortiert, falls $k\le l \iff \my(p_k)+\ny(p_k)\le \my(p_l)+\ny(p_l)$.

Jede MiMa-Sortierung ist sowohl eine Mi- als auch eine Ma-Sortierung.