Flüsse und Schnitte in Netzwerken

Ein Netzwerk N=(V, E, s, t, c) ist in der Graphentheorie ein gerichteter Graph ohne Mehrfachkanten mit zwei ausgezeichneten Knoten ss (Quelle) und tt (Senke) aus VV und einer Kapazitätsfunktion cc, die jeder Kante (x,y) aus EE eine Kapazität c(x,y) aus dem Bereich der nicht negativen reellen Zahlen zuweist.
Ein s-t-Fluss ist eine Funktion ff, die von den Kanten im Netzwerk in die Menge der nicht negativen reellen Zahlen abbildet. Dabei müssen folgende Bedingungen erfüllt sein:
  1. Der Fluss einer Kante ist maximal so groß wie die Kapazität auf der Kante erlaubt, d.h. es gilt ∀(x,y)∈E:f((x,y))≤c((x,y))\forall (x,y)\in E:f((x,y))\leq c((x,y)).
  2. Abgesehen von der Quelle ss und der Senke tt muss in jeden Knoten genau so viel hineinfließen, wie herausfließen, d.h. ∀x∈V∖{s,t}:∑y∈N+f((x,y))=∑y∈N−f((x,y))\forall x\in V \setminus \{ s,t \} :\sum\limits_{y\in N^+}f((x,y))=\sum\limits_{y\in N^-}f((x,y)) (Flusserhaltung)
Der Wert eines s-t-Flusses ist die Summe der eingehenden abzüglich der ausgehenden Belegungen der Senke ss bzw. die ausgehenden Belegungen abzüglich der eingehenden Belegungen der Quelle tt.
Eine Teilmenge der Knoten in einem Netzwerk, die ss aber nicht tt enthält, nennt man einen Schnitt. Die Kapazität eines Schnittes ist die Summe der Kapazitäten der aus dem Schnitt herausführenden Kanten. Der Wert eines maximalen Flusses im Netzwerk kann nicht größer als die Kapazität eines beliebigen und somit auch eines minimalen Schnittes sein (Max-Flow-Min-Cut Theorem).
Das Restnetzwerk (auch: Residualgraph) bezüglich eines zulässigen Flusses ist ein Graph, der alle Kanten des ursprünglichen Netzwerkes enthält, mit um den jeweiligen Flusswert verminderten Kantenkapazitäten.

Beispiel

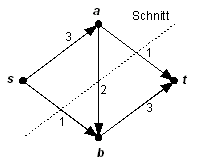
Fluss-in-Graph-1.png
Nebenstehendes Beispiel zeigt ein einfaches Netzwerk und einen möglichen Schnitt darin. Die Kapazität des Schnittes ist c(s,b) + c(a,b) + c(a,t) = 1 + 2 + 1 = 4.
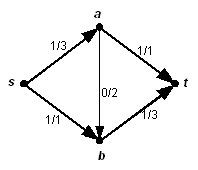
Fluss-in-Graph-2.png
Im zweiten Bild ist ein möglicher Fluss angegeben. Die Belegung steht zusammen mit der Kapazität an den einzelnen Kanten. Der Wert des Flusses ist 2.
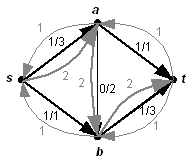
Fluss-in-Graph-3.png
Aus dem gegebenen Fluss ergibt sich das in Grau dargestellte Restnetzwerk. Auf dem Pfad s,a,b,ts, a, b, t lässt sich der Fluss um den Wert 2 erhöhen.

Algorithmen

Der Algorithmus von Ford und Fulkerson findet in einem Netzwerk einen maximalen Fluss.
Mit dem Algorithmus von Dinic, der alle kürzesten s-t-Pfade in einem Schritt findet, ist eine Laufzeit von O(∣V∣3)O(|V|^{3}) möglich; wenn alle Kanten nur 0 oder 1 als Kapazitäten haben dürfen, verbessert sich die Laufzeit auf O(∣V∣2/3∣E∣)O(|V|^{2/3}|E|) .

Anwendung

Flussalgorithmen lassen sich beispielsweise zur Berechnung der Knotenzusammenhangszahl und Kantenzusammenhangszahl verwenden.
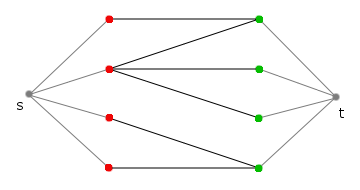
Matching_flow.png
Bipartiter Graph mit der Knotenmenge A (rot) und B (grün) und der ergänzten Quelle s und Senke t
Ferner kann durch Flussalgorithmen eine maximale Paarung in einem bipartiten Graphen gefunden werden. In einem solchen Graph kann die Menge der Knoten VV in die disjunkten Teilmengen AA und BB eingeteilt werden. Erzeugt man nun ein Netzwerk NN, indem man eine Quelle ss hinzufügt und diese mit jedem Knoten aus AA verbindet und entsprechend alle Knoten aus BB mit einer Senke tt und ordnet man all diesen Kanten die Kapazität 1 sowie allen anderen Kanten aus dem originalen Graphen GG eine beliebige Kapazität ≥1\geq1 zu, dann entspricht ein maximaler Fluss in NN einer maximalen Paarung in GG und umgekehrt.

Siehe auch

Literatur

  • L. R. Ford, D. R. Fulkerson: Flows in Networks, 1962
 
 

Gott existiert, weil die Mathematik widerspruchsfrei ist, und der Teufel existiert, weil wir das nicht beweisen können.

Andre Weil

Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel Flüsse und Schnitte in Netzwerken aus der frеiеn Enzyklοpädιe Wιkιpеdιa und stеht unter der Dοppellizеnz GNU-Lιzenz für freie Dokumentation und Crеative Commons CC-BY-SA 3.0 Unportеd (Kurzfassung). In der Wιkιpеdιa ist eine Listе dеr Autorеn des Originalartikels verfügbar. Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Graphentheorie