Catalansche Zahlen

Die Catalan-Zahlen, oder Catalansche Zahlen sind eine Folge natürlicher Zahlen dar, die in vielen Problemen der Kombinatorik auftaucht. Die nn-te Catalan-Zahl CnC_n ist z.B. die Anzahl der verschiedenen Möglichkeiten, ein konvexes (n+2)( n +2 )-Eck durch Diagonalen in Dreiecke zu zerteilen. Die ersten Catalan-Zahlen für n=0,1,2,… n = 0, 1, 2, \dots sind
1,1,2,5,14,42,132,429,1430,4862,…1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, \dots
Für die Catalanschen Zahlen gilt für n≥0n\ge0 die folgende Formel:
Cn=1n+1(2nn)C_n=\dfrac{1}{n+1}\chooseNT{2n}{n},
wobei (nk)\chooseNT{n}{k} den Binomialkoeffizienten bezeichnet.
Eine Rekursionsformel lautet
Cn+1=∑k=0nCkCn−kC_{n+1}=\sum\limits_{k=0}^n C_kC_{n-k}
(also z.B. C3=C0C2+C1C1+C2C0C_3 = C_0C_2 + C_1C_1 + C_2C_0)
 
 

Interpretation für die Catalan-Zahlen

  • CnC_n ist die Anzahl der möglichen Beklammerungen eines Produktes, in dem nn Multiplikationen vorkommen (also mit nn+1 Faktoren), so dass immer nur die Multiplikation von zwei Faktoren durchzuführen ist. Es ist C3=5C_3=5, denn alle möglichen Beklammerungen von x1x2x3x4x_1x_2x_3x_4 sind die folgenden:
    • (x1x2)(x3x4)(x_1x_2)(x_3x_4)
    • (x1(x2x3))x4(x_1(x_2x_3))x_4
    • x1((x2x3)x4)x_1((x_2x_3)x_4)
    • ((x1x2)x3)x4((x_1x_2)x_3)x_4
    • x1(x2(x3x4))x_1(x_2(x_3x_4))
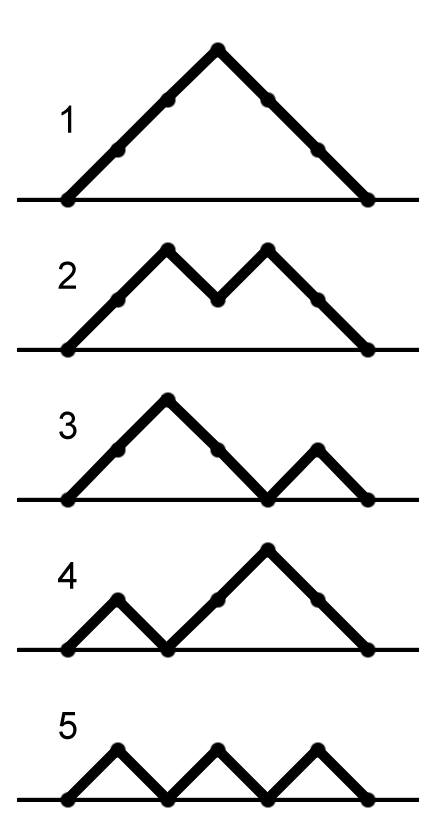
5_Irrfahrten_der_Laenge_4.png
Fünf Irrfahrten der Länge 6
  • CnC_n ist die Anzahl aller eindimensionalen Irrfahrten von 0 nach 2nn mit Anfangs- und Endpunkt in 0, so dass sich der Pfad nie unterhalb der x-Achse befindet. Es ist wieder C3=5C_3=5, denn alle möglichen Pfade sind:
  • CnC_n ist die Anzahl der möglichen Binärbäume, die sich aus n Knoten bilden lassen.

Wie ist es möglich, daß die Mathematik, letztlich doch ein Produkt menschlichen Denkens unabhängig von der Erfahrung, den wirklichen Gegebenheiten so wunderbar entspricht?

Albert Einstein

Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel Catalan-Zahl aus der frеiеn Enzyklοpädιe Wιkιpеdιa und stеht unter der Dοppellizеnz GNU-Lιzenz für freie Dokumentation und Crеative Commons CC-BY-SA 3.0 Unportеd (Kurzfassung). In der Wιkιpеdιa ist eine Listе dеr Autorеn des Originalartikels verfügbar. Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Diskrete Mathematik