Differentialgleichungen der Gestalt $y'=f(ax+by+c)$ lösen wir mittels der Substitution $z=ax+by+c$. Dann ist $z'=\dfrac{\d z}{\d x}=a+by'$ $\implies z'=a+bf(z)$. Dies ist eine Differentialgleichung mit getrennten Variablen: $\dfrac {\d z}{a+bf(z)}=\d x$.

$y'=2x-3y+1$. Substitution $z=2x-3y+1$, $z'=2-3y'$ $\implies z'=2-3z$.

$\int\limits\dfrac {\d z} {2-3z}=\int\limits \d x$ $\implies -\dfrac 1 3 \ln|2-3z|=x+C_0$ $\implies \ln|2-3z|=-3x+C_1$ $\implies 2-3z=\e^{-3x}\cdot C_2$ ($C_2>0$) $\implies 2-3(2x-3y+1)$ $=2-6x+9y-3$ $=\e^{-3x}\cdot C_2$ $\implies 9y=\e^{-3x}\cdot C_2+6x+1$ $\implies y=\dfrac {\e^{-3x}\cdot C_2} 9+\dfrac 2 3 x+\dfrac 1 9$

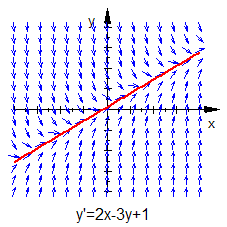
Mit einer Probe überzeugen wir uns, schnell, dass wir eine Lösung gefunden haben. Leider ist uns die Lösung $y=\dfrac 2 3 x+\dfrac 1 9$ (rote Gerade in der Grafik) verloren gegangen. Da stets $C_2>0$ und auch $\e^{-3x}\cdot C_2>0$ ist, ist sie in der Formel nicht enthalten. Wir erhalten sie jedoch als asymptotischen Grenzfall für $C_2\to 0$.