Spannbaum
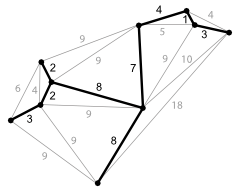
Ein Graph mit einem minimalen Spannbaum.
Ein Spannbaum (auch aufspannender Baum oder spannender Baum genannt; englisch spanning tree) ist in der Graphentheorie ein Teilgraph eines ungerichteten Graphen, der ein Baum ist und alle seine Knoten enthält. Spannbäume existieren nur in zusammenhängenden Graphen.
Einen Teilgraphen, der in (nicht notwendigerweise zusammenhängenden) Graphen für jede Komponente einen Spannbaum ergibt, nennt man Gerüst, Spannwald, aufspannender Wald oder kürzer spannender Wald. In zusammenhängenden Graphen sind Gerüst und Spannbaum also identische Begriffe, während Spannbäume für unzusammenhängende Graphen nicht definiert sind.
In kantengewichteten Graphen lässt sich als Gewicht eines Graphen die Summe seiner Kantengewichte definieren. Ein Spannbaum bzw. ein Gerüst heißt minimal, wenn kein anderer Spannbaum bzw. kein anderes Gerüst in demselben Graphen mit geringerem Gewicht existiert. Häufig kürzt man minimaler Spannbaum auch mit MST (Abkürzung des englischen Begriffs Minimum Spanning Tree) oder MCST (Minimum Cost Spanning Tree - ein Spannbaum mit minimalen Kosten) ab. Statt minimales Gerüst sagt man auch Minimalgerüst.
Das Spannbaumproblem tritt in der Praxis beispielsweise bei der kürzesten Verdrahtung von Kommunikationsnetzen auf (siehe auch Spanning Tree Protocol). Für das Problem des Handlungsreisenden existieren Approximationsalgorithmen, die minimale Spannbäume verwenden.
Wichtige Algorithmen
Zum Finden eines minimalen Spannbaumes gibt es den Algorithmus von Kruskal, den Algorithmus von Prim, der Worst-Case-Laufzeit besitzt. Dieser benötigt aber mit Fibonacci-Heaps eine recht komplexe Datenstruktur. Man kann zeigen, dass der Algorithmus von Prim damit im Wesentlichen bestmöglich ist, da man mit seiner Hilfe auch Zahlen sortieren kann.
Anwendungen
Die Berechnung minimaler Spannbäume findet direkte Anwendungen in der Praxis, wenn man zum Beispiel kostengünstig zusammenhängende Netzwerke (z.B. Telefonnetzwerke, elektrische Netzwerke u.a.) herstellen will oder bei Computernetzwerken mit Redundanz, wo das Spanning Tree Protocol zur Anwendung kommt.
In der Graphentheorie selbst sind MST-Algorithmen häufig Grundlage komplexerer Algorithmen für schwierigere Probleme. Die Berechnung minimaler Spannbäume ist zum Beispiel Bestandteil von Approximationsalgorithmen für das Steinerbaum-Problem oder für das Problem des Handlungsreisenden (oft auch Traveling-Salesman-Problem genannt und TSP abgekürzt).
Insofern sich die Sätze der Mathematik auf die Wirklichkeit beziehen, sind sie nicht sicher, und insofern sie sicher sind, beziehen sie sich nicht auf die Wirklichkeit.
Albert Einstein
Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel
Spannbaum
aus der frеiеn Enzyklοpädιe Wιkιpеdιa
und stеht unter der Dοppellizеnz
GNU-Lιzenz für freie Dokumentation und
Crеative Commons CC-BY-SA 3.0 Unportеd
(Kurzfassung).
In der Wιkιpеdιa ist eine
Listе dеr Autorеn
des Originalartikels verfügbar.
Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld
• Dοrfplatz 25 • 17237 Blankеnsее
• Tel.: 01734332309 (Vodafone/D2) •
Email: cο@maτhepedιa.dе