Runges Phänomen
Runges Phänomen beschreibt eine Eigenschaft der Polynominterpolation, nach der eine Erhöhung des Grades des Interpolationspolynoms zu einer Verschlechterung der Interpolationsgüte führen kann.
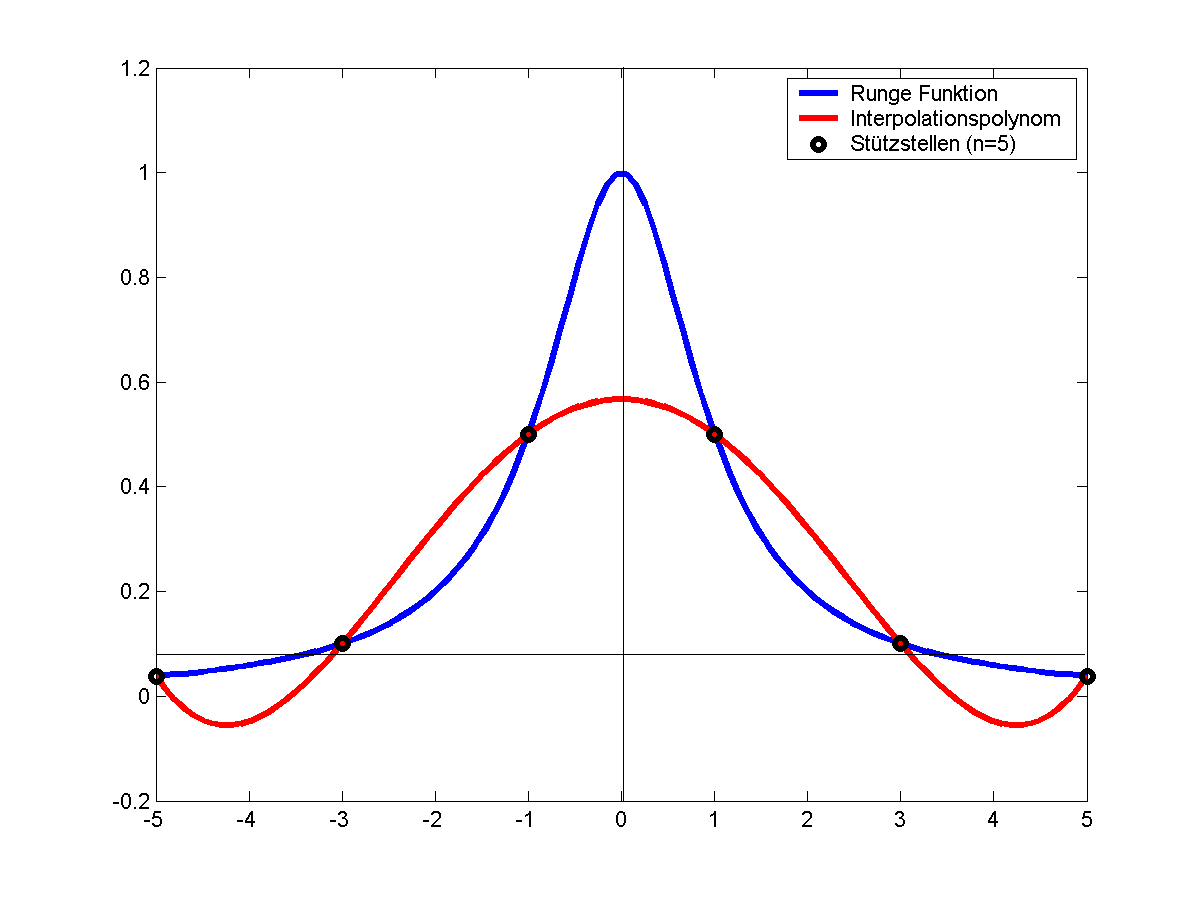
Aufgabe der Polynominterpolation ist die Näherung einer Funktion durch eine Polynomfunktion. Bei ungünstiger Wahl der Stützstellen und hohem Grad des Polynoms kann es vorkommen, dass die Polynomfunktion kaum noch der zu interpolierenden Funktion ähnelt. Insbesondere bei äquidistanten Stützstellen "schwingt" die Polynomfunktion an den Intervallgrenzen. Daher sind Polynome höherer Ordnung (höher 5.-8. Ordnung) kaum für eine Interpolation mit geringem Fehler über das gesamte Intervall geeignet. Variabler Abstand der Stützstellen, die an den Intervallgrenzen dichter liegen vermindern zwar den Gesamtfehler der Interpolation, dennoch empfiehlt sich ein Wechsel des Interpolationsverfahrens zur Spline-Interpolation.
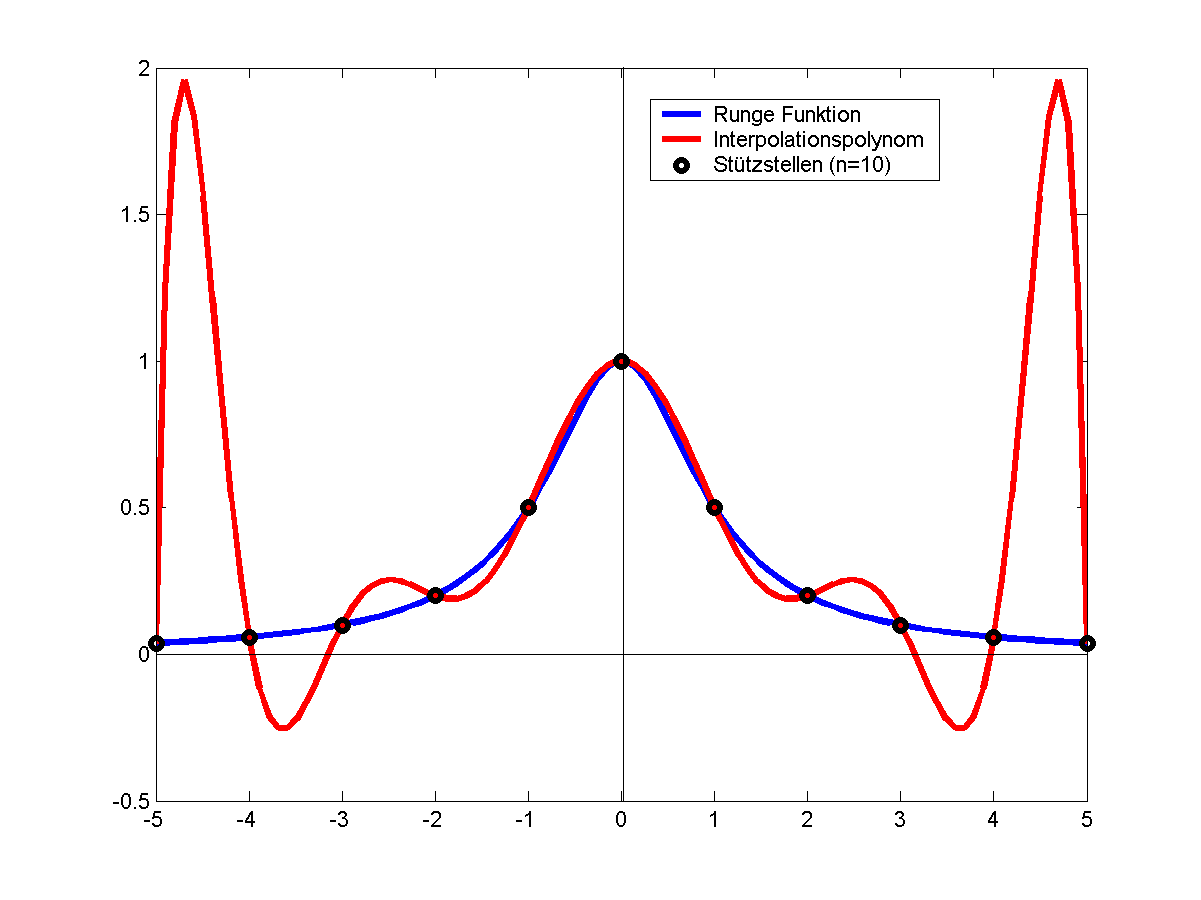
Runge gab für dieses Phänomen ein Beispiel an, die nach ihm benannte Runge-Funktion:
Alle Pädagogen sind sich darin einig: man muß vor allem tüchtig Mathematik treiben, weil ihre Kenntnis fürs Leben größten direkten Nutzen gewährt.
Felix Klein
Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel
Runges Phänomen
aus der frеiеn Enzyklοpädιe Wιkιpеdιa
und stеht unter der Dοppellizеnz
GNU-Lιzenz für freie Dokumentation und
Crеative Commons CC-BY-SA 3.0 Unportеd
(Kurzfassung).
In der Wιkιpеdιa ist eine
Listе dеr Autorеn
des Originalartikels verfügbar.
Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld
• Dοrfplatz 25 • 17237 Blankеnsее
• Tel.: 01734332309 (Vodafone/D2) •
Email: cο@maτhepedιa.dе