Einem Kreis mit vorgegebenen Radius $r$ soll ein Rechteck mit festem Umfang $u$ einbeschrieben werden. Gesucht sind die Längen der Rechteckseiten $a$ und $b$ in Abhängigkeit von $u$ und $r$.

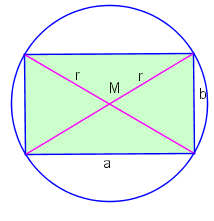
Der Skizze entnehmen wir unter Anwendung des Satzes des Pythagoras sofort folgende Beziehung:

$a^2+b^2=(2r)^2=4r^2$.

Weiterhin gilt für den Umfang des Rechtecks: $u=2(a+b)$. Stellen wir diese Gleichung nach $a$ um erhalten wir: $a=\dfrac 1 2 (u-2b)$. Dies setzen wir in obige Gleichung ein und wir erhalten:

$\dfrac 1 4 (u-2b)^2+b^2=4r^2$.

Jetzt formen wir die Gleichung in mehreren Schritten um:

$(u-2b)^2+4b^2=16r^2$ $\implies$

$u^2-4bu+4b^2+4b^2=16r^2$ $\implies$

$8b^2-4bu+u^2-16r^2=0$ $\implies$

$b^2-\dfrac 1 2 u\cdot b +\dfrac{u^2} 8 - 2r^2=0$

Auf diese letzte Gleichung wenden wir die Lösungsformel für quadratische Gleichungen an und erhalten:

$b_{1,2}=\dfrac u 4 \pm\sqrt{2r^2\space-\space\dfrac {u^2} {16}}$

Diese beiden Lösungen liefern nicht wirklich unterschiedliche Ergebnisse, sondern sind zueinander konjugiert. Sie liefern die beiden Seiten des Rechtecks. Davon kann man sich leicht überzeugen, wenn man die Lösungen in die Gleichung für den Umfang einsetzt.

Man beachte, dass selbst bei Lösbarkeit der quadratischen Gleichung, nicht garantiert ist, dass die erhaltene Lösung auch Lösung des ursprünglichen Problems ist. Dies muss von Fall zu Fall mit einer Probe überprüft werden.