Beispiel zu Äquivalenzrelationen (Hyperbeln)

Für

(x,y),(x',y')\in \dom {R^2}

definieren wir:

(x,y)\sim (x',y'):\iff\exists t\in \dom {R^+}: x'=tx, \space y'=\dfrac y t

Wir zeigen, dass die so definierte Relation eine Äquivalenzrelation ist.

t=1

trivial erfüllt.

Um zu zeigen, dass die Relation symmetrisch ist, formen wir sie etwas um. Die obige Definition ist nämlich äquivalent zu folgender:

(x,y)\sim (x',y'):\iff xy=x'y'

Damit ist die Relation offensichtlich symmetrisch und die Transitivität erhält man auf Grund der Transitivität der Gleichheit.

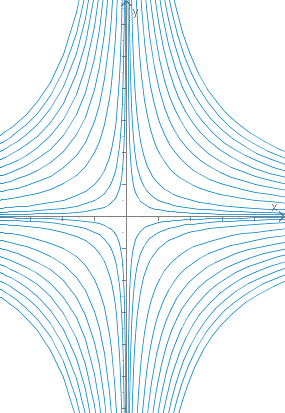
Versuchen wir jetzt die Äquivalenzklassen der obigen Relation zu beschreiben. Nach dem Hauptsatz über Äquivalenzrelationen müssen diese eine Zerlegung des

\dom {R^2}

bilden.

Für ein

c\in\dom R

können wir die zugehörige Äquivalenzklasse durch

P_c=\{(x,y)| \space xy=c\}

beschreiben.

Für

c=0

ergeben sich genau alle auf den Koordinatenachsen liegenden Punkte, denn um die Gleichung zu erfüllen, muss

x=0

oder

y=0

gelten.

Für

c\neq 0

kann die Gleichung nur erfüllt werden, wenn

x\neq 0

und

y\neq 0

gilt; wir können die Gleichung also in der Form

y=\dfrac c x

schreiben.

Damit sind die Äquivalenzklassen genau die gestreckten/gestauchten Einheitshyperbeln.

Als zusätzliches Ergebnis erhalten wir:

Wenn

c_1\neq c_2

dann haben die (eventuell entarteten) Hyperbeln

xy=c_1

und

xy=c_2

keine Punkte gemeinsam.

Dies folgt sofort aus der Zerlegungseigenschaft von Äquivalenzrelationen.

Die ganzen Zahlen hat der liebe Gott geschaffen, alles andere ist Menschenwerk.

Leopold Kronecker

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.

Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld • Dοrfplatz 25 • 17237 Blankеnsее • Tel.: 01734332309 (Vodafone/D2) • Email: cο@maτhepedιa.dе