Parallelenbüschel und Geradenbüschel
Satz DY88
Beweis
Wegen Satz UK27 bleibt nur noch die Transitivität zu zeigen. Seien nun , und drei Geraden. Angenommen zwei von ihnen sind gleich, dann gilt die Transitivität trivial. Seien die drei Geraden nun paarweise verschieden und es gelte und . Angenommen , dann gibt es nach Satz UU90 genau einen Schnittpunkt . Dieser liegt nach Definition der Parallelität nicht auf . Es gibt aber zwei parallele Geraden zu , die durch gehen, nämlich und , was im Widerspruch zum Parallelenaxiom ist.
Die Äquivalenzklassen bezüglich der Parallelität nennen wir Parallelenbüschel oder Richtung. Das Parallelenbüschel zu einer Geraden bezeichnen wir mit und es gilt:
In Analogie definieren wir ein Geradenbüschel zu einem Punkt als die Menge aller geraden, die enthält:
Beispiele
Abb. BT41 zeigt Beispiele für Parallelen- und Geradenbüschel in unserer Anschauungsebene.
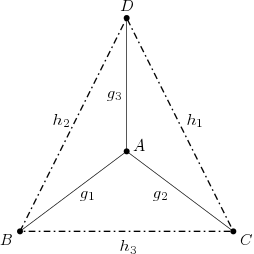
Abb. QN68: Minimale affine Ebene
In der minimalen affinen Ebene aus Beispiel UI60 gibt es zwei Parallelenbüschel, eins mit den -Geraden und eins mit den -Geraden. In Abb. QN68 sind diese durch unterschiedliche Linienstile hervorgehoben.
Satz RD73
In einer affinen Ebene seien , und drei Punkte in allgemeiner Lage. Dann sind die drei Parallelenbüschel , und paarweise verschieden.
Beweis
Angenommen und damit . Nun gilt und , also , was aber mit der Definition der Parallelität bedeutet, dass gilt. Nach Satz WI24 ist damit im Widerspruch zur Annahme, dass die drei Punkte in allgemeiner Lage sind.
Satz KS67
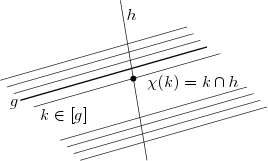
Seien und nicht parallele Geraden einer affinen Ebene und die folgende Abbildung von der Menge aller zu parallelen Geraden in die Menge der Punkte der Geraden :
für .
Dann gilt ist eine Bijektion. Damit können dann je zwei Geraden bijektiv aufeinander abgebildet werden.
Beweis
Da und nicht parallel sind (sie gehören zu verschiedenen Äquivalenzklassen), gibt es nach Satz UU90 einen eindeutig bestimmten Schnittpunkt , also ist wohldefiniert.
Es gelte für , also . Nach dem Parallelenaxiom ist die Parallele zu durch eindeutig. liegt auf dieser Parallele und auf und , daher gilt , womit gezeigt ist, dass injektiv ist. Sei ein Punkt der Geraden . Es gibt nach Parallelenaxiom eine Gerade mit und , also gilt . Für jeden Punkt gibt es ein Urbild, also ist ist surjektiv.
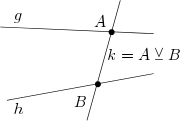
Abb. QB07: Zum Beweis von Satz KS67
Zwei identische Geraden und können sicher bijektiv aufeinander abgebildet werden. Sei nun . Dann gibt es nach Satz NF12 einen Punkt mit und einen Punkt mit und (vgl. Abb. QB07). Diese Punkte sind offensichtlich verschieden und ihre Verbindungsgerade ist wohldefiniert. Außerdem ist wegen und wegen . Damit gibt es nach dem oben Bewiesenen Bijektionen und . Die Abbildung ist nach Satz 15XJ eine Bijektion, die und aufeinander abbildet.
Wie ist es möglich, daß die Mathematik, letztlich doch ein Produkt menschlichen Denkens unabhängig von der Erfahrung, den wirklichen Gegebenheiten so wunderbar entspricht?
Albert Einstein
Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf
ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld
• Dοrfplatz 25 • 17237 Blankеnsее
• Tel.: 01734332309 (Vodafone/D2) •
Email: cο@maτhepedιa.dе
Synthetische Geometrie
- Inzidenzebenen
- Affine Ebenen
- Parallelenbüschel und Geradenbüschel
- Dilatationen
- Projektive Ebenen
- Absolute Ebenen
