Abbildungen und Funktionen

Abb.png
Eine beliebige Teilmenge f⊆X×Yf\subseteq X\cross Y des kartesischen Produkts zweier Mengen XX und YY heißt Abbildung oder Funktion, falls ff eindeutig ist, also einem Element x∈Xx\in X durch ff höchstens ein Element y∈Yy\in Y zugeordnet wird. Formal:
f⊆X×Yf \subseteq X\cross Y ist Abbildung   ⟺  ∀x,y1,y2:(x,y1)∈F∧(x,y2)∈F  ⟹  y1=y2\iff \forall x,y_1,y_2: (x,y_1)\in F \and (x,y_2) \in F \implies y_1=y_2
Damit sind Funktionen nichts anderes als eindeutige 2-stellige Relationen.
Man schreibt dann
f:X→Yf: X\to Y,
und mit x∈Xx\in X und y∈Yy\in Y symbolisiert man die Zuordnung durch
x↦yx\mapto y bzw. y=f(x)y=f(x).
Man nennt xx die unabhängige Variable und yy die abhängige Variable.
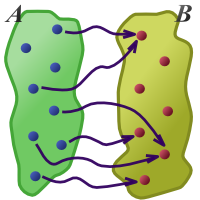
Die Grafik rechts verdeutlicht das Wesen der Abbildung. Die Zuordnungen sind durch Pfeile symbolisiert. Von jedem Element der linken Menge geht höchstens ein Pfeil aus.
 
 

Definitionen

Sei nun f:X→Yf:X\to Y eine Abbildung und x∈Xx\in X, y∈Yy\in Y mit y=f(x)y=f(x). yy heißt das Bild oder der Funktionswert von xx. Andererseits wird xx das Urbild von yy genannt. Da ff eine Abbildung ist, ist das Bild immer eindeutig bestimmt, falls es definiert ist. Das Urbild hingegen muss - falls definiert - nicht eindeutig sein.
Wir bezeichnen die Menge aller Urbilder eines Funktionswertes mit Df(y)={x∈X∣y=f(x)}D_f(y)=\{x\in X| y=f(x)\} und für B⊂YB\subset Y analog Df(B)={x∈X∣∃y∈Y:y=f(x)}D_f(B)=\{x\in X| \exists y\in Y : y=f(x)\} =⋃y∈BDf(y)=\bigcup\limits_{y\in B}D_f(y).
Der Definitionsbereich (Argumentbereich/ Urbildbereich) D(f)=Df:=Df(Y)D(f)=D_f\eqdef D_f(Y) von ff ist die Menge aller Urbilder. Klar ist, dass Df⊆XD_f\subseteq X gilt. (Teilweise sieht man auch die Bezeichnung dom(f)\Domain(f) für DfD_f.)
Für einer Teilmenge A⊆XA\subseteq X heißt f(A)⊆Yf(A)\subseteq Y analog das Bild von AA.
Der Bildbereich oder Wertebereich Wf=W(f):=f(X)W_f=W(f)\eqdef f(X) von ff ist die Menge aller Bilder:
Wf:={y∈Y∣ ∃x∈X:y=f(x)}W_f:=\{y\in Y| \space \exists x\in X: y=f(x)\}.
An Stelle von WfW_f sieht man auch die Bezeichnung im(f)\Image(f).

Beispiele

Die lineare Funktion y=xy=x besitzt als Definitionsbereich und Wertebereich die reellen Zahlen.
Die quadratische Funktion y=x2y=x^2 besitzt als Definitionsbereich auch alle reellen Zahlen aber als Wertebereich die nichtnegativen reellen Zahlen. Es gilt f(2)=4f(2)=4, also ist 44 Bild von 22. Das Urbild von 44 ist jedoch die zweielementige Menge {2,−2}\{2,-2\}.
Bei der Wurzelfunktion y=xy=\sqrt x umfasst sowohl der Definitionsbereich als auch der Wertebereich nur die nichtnegativen Zahlen.

Gleichheit von Abbildungen

Für die Gleichheit zweier Funktionen ff und gg können wir festhalten:
f=g  ⟺  Df=Dgf=g \iff D_f=D_g ∧∀x:x∈Df  ⟹  f(x)=g(x)\and \forall x: x\in D_f \implies f(x)=g(x)
Die Forderung, dass auch die Definitionsbereiche übereinstimmen müssen, wird schnell übersehen und meist durch die Forderung des Übereinstimmens der Funktionswerte impliziert. Da aber im Allgemeinen DfD_f eine echte Teilmenge von XX ist, muss man sehr wohl überprüfen, ob die Funktionswerte beider Funktionen jeweils existieren. Ist dies gesichert folgt daraus wiederum, dass ihre Definitionsbereiche übereinstimmen müssen.

Seit die Mathematiker über die Relativitätstheorie hergefallen sind, verstehe ich sie selbst nicht mehr.

Albert Einstein

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Grundlagen der Mathematik