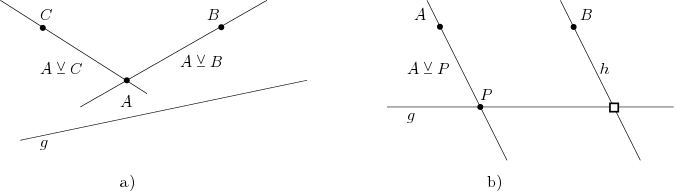Affine Ebenen

Parallelität

Zwei verschiedene Geraden gg und hh heißen parallel g ∥ hg\para h, wenn sie übereinstimmen oder keinen Punkt gemeinsam haben:
g ∥ h  ⟺  g=h ∨ g∩h=∅g\para h\iff g=h\,\vee\, g\cap h=\OO.
Wir schreiben g ∦ hg\npara h falls gg und hh nicht parallel sind.
Mit dieser Definition kann Satz SU09 auch wie folgt formuliert werden: zwei Geraden sind entweder parallel oder sie haben einen Schnittpunkt bzw:
 
 

Satz UU90

Zwei nicht parallele Geraden einer Inzidenzstruktur haben genau einen Schnittpunkt.

Beweis

Ergibt sich direkt aus Satz SU09 und der Definition der Parallelität. □\qed

Satz UK27

In einer Inzidenzstruktur ist die Parallelität eine eine reflexive und symmetrische Relation.

Beweis

Mit g=gg=g gilt sicher g ∥ gg\para g und die Parallelität ist reflexiv.
g ∥ h  ⟹  g=hg\para h\implies g=h oder g∩h=∅  ⟹  h=gg\cap h=\OO\implies h=g oder h∩g=∅  ⟹  h ∥ gh\cap g=\OO\implies h\para g, womit die Parallelität symmetrisch ist. □\qed

Satz PW02 (Kollineationen erhalten die Parallelität)

Sei φ\varphi eine Kollineation, dann gilt für beliebige Geraden gg und hh: aus g ∥ hg\para h folgt φ(g) ∥ φ(h)\varphi(g)\para\varphi(h).

Beweis

Für g=hg=h gilt die Behauptung trivial. Sei also g≠hg\ne h und φ(g) ∦ φ(h)\varphi(g)\npara\varphi(h), dann gibt es nach Satz UU90 einen Punkt P=φ(g)∩φ(h)P=\varphi(g)\cap\varphi(h), also muss φ−1(P)∈g,h\varphi^{-1}(P)\in g,h, im Widerspruch zu g ∥ hg\para h. □\qed

In der minimalen affinen Koordinatenebene aus Beispiel CK37 gilt gi ∥ hig_{i}\para h_{i} für i=1,2,3i=1,2,3. Es gibt also zwei Klassen mit jeweils 3 parallelen Geraden. Dies ist kein Zufall, denn es gilt:

Das Parallelenaxiom

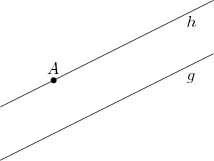
ParAx.png
Abb. KB50: Veranschaulichung des Parallelenaxioms
In der minimale Inzidenzebene aus Beispiel AJ15 gibt es keine verschiedenen parallelen Geraden, da je zwei Geraden einen Punkt gemeinsam haben. Man fordert jedoch die Existenz bestimmter Parallelen zu existierenden Geraden.
ParAx: Zu jedem Punkt AA und jeder Gerade gg gibt es genau eine parallele Gerade hh, auf der AA liegt, also h ∥ gh\para g und A∈hA\in h.
Eine Inzidenzebene, in der das Parallelenaxiom gilt, heißt affine Ebene. Die parallele Gerade zu einer Gerade gg durch einen Punkt PP wird im Folgenden mit P∥‾gP\parad g bezeichnet.

Beispiel UI60 (Minimale affine Ebene)

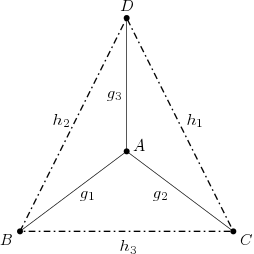
MinAffGeo.png
Abb. UT85: Minimale affine Ebene
Die minimale Inzidenzebene aus Beispiel AJ15 ist keine affine Ebene. Wie sieht nun die minimale affine Ebene aus? Sie muss mindestens 4 Punkte enthalten. Betrachten wir also eine Struktur mit vier Punkten, wo die Geraden alle Punktepaare sind, so ist dies nach Beispiel AV45 eine Inzidenzebene. Sie ist in Abb. UT85 veranschaulicht. Es gilt gk ∥ hkg_{k}\para h_{k} für k=1,2,3k=1,2,3. Es gilt das Parallelenaxiom, denn zu jeder Geraden gkg_{k} gibt es genau eine Parallele hkh_{k} und diese ist dann die Parallele für jeweils zwei nicht auf gkg_{k} liegende Punkte. Damit haben wir auch ein Modell für eine affine Inzidenzebene gefunden. Diese affine Ebene ist isomorph zur minimalen affinen Koordinatenebene aus Beispiel CK37.

Beispiel

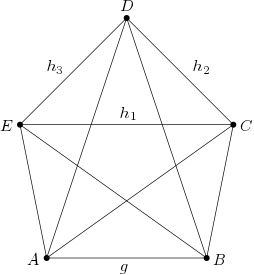
MehrParallelen.png
Abb. HQ71: Inzidenzebene, in der das Parallelenaxiom nicht gilt
Dieses Beispiel zeigt, dass es auch mehrere parallele Geraden durch einen Punkt zu einer vorgegebenen Gerade geben kann. Wir betrachten die Inzidenzstruktur aus Abb. HQ71, die der Inzidenzebene aus Beispiel AV45 mit fünf Punkten entspricht. (Die Geraden sind genau die Punktepaare.) Zur Geraden gg gibt es nun drei parallele Geraden h1h_{1},h2h_{2} und h3h_{3}, die sich jeweils paarweise in einem Punkt schneiden. Damit gibt es zum Punkt DD, der nicht auf gg liegt, zwei parallele Geraden zu gg, die DD enthalten, nämlich: h2h_{2} und h3h_{3}.

Das Parallelenaxiom ist nicht unabhängig von den drei Inzidenzaxiomen, es gilt:

Satz KR98

Aus Inz1, Inz3 und ParAx folgt Inz2.

Beweis

Angenommen es gelten Inz1, Inz3, ParAx und nicht Inz2. Wir werden dies zu einem Widerspruch führen. Nicht Inz2 bedeutet, dass es eine Gerade mit weniger als zwei Punkten gibt. Dazu unterscheiden wir nun zwei Fälle. Zur Veranschaulichung der beiden Fälle dient Abb. RX83.
InzParUnabh.png
Abb. RX83: Zum Beweis von Satz KR98 a) Fall 1 mit einer Gerade gg ohne Punkte, b) Fall 2 mit einer Geraden gg mit genau einem Punkt PP.
Fall 1: Es gibt eine Gerade gg ohne Punkte. Nach Inz3 gibt es drei Punkte AA, BB und CC in allgemeiner Lage und nach Inz1 gibt es durch jeweils zwei von ihnen eine eindeutig bestimmte Gerade. Diese Geraden haben mit gg keine gemeinsamen Punkte, da gg ja keine Punkte enthält, damit sind sie alle zu gg parallel. Der Punkt AA liegt auf den Verbindungsgeraden A ⊻ BA\vgr B und A ⊻ CA\vgr C, damit ist aber das Parallelenaxiom verletzt, da es zwei parallele Geraden zu gg gibt, die durch AA gehen.
Fall 2: Es gibt eine Gerade gg mit genau einem Punkt PP.
Dann gibt es nach Satz JO42 zwei Punkte AA und BB, sodass diese mit PP in allgemeiner Lage sind. Nach Inz1 existiert für AA und PP die Verbindungsgerade A ⊻ PA\vgr P. Nach ParAx gibt es genau eine parallele Gerade hh zur Verbindungsgerade A ⊻ PA\vgr P durch den Punkt BB. Wegen dieser Parallelität liegt PP nicht auf hh und da gg nur den Punkt PP enthält, haben gg und hh keine Punkte gemeinsam, sind nach Definition also parallel. Damit sind sowohl gg als auch die Verbindungsgerade A ⊻ PA\vgr P zwei verschiedene zu hh parallele Geraden durch PP im Widerspruch zu ParAx. □\qed
Damit können wir in affinen Ebenen ein Axiom einsparen und diese nur durch Inz1, Inz3 und ParAx axiomatisieren.

Satz DT42 (Unabhängigkeit der Axiome der affinen Ebene)

Die drei Axiome Inz1, Inz3 und ParAx sind unabhängig voneinander.

Beweis

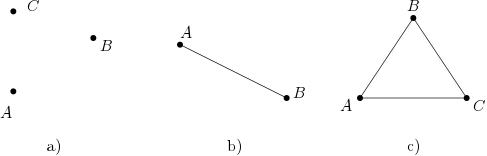
AffUnabh.png
Abb. QT71: Zur Unabhängigkeit der Axiome der affinen Ebene (Satz DT42).
Die isolierten drei Punkte aus Abb. QT71 a) liefern ein Beispiel, in dem Inz3 und ParAx gelten (das Parallelenaxiom trivial, da es gar keine Geraden gibt) jedoch Inz1 nicht.
Abb. QT71 b) zeigt ein Beispiel, das Inz3 verletzt, da es nur die beiden Punkte AA und BB gibt. Sie sind durch eine Gerade verbunden, womit Inz1 gilt und da es keinen weiteren Punkt gibt, gilt ParAx offensichtlich.
Die minimale Inzidenzebene aus Beispiel AJ15 - siehe Abb. QT71 c) - erfüllt Inz1 und Inz3. Es schneiden sich jedoch jeweils zwei Geraden, also gilt ParAx nicht. □\qed

Seit man begonnen hat, die einfachsten Behauptungen zu beweisen, erwiesen sich viele von ihnen als falsch.

Bertrand Russell

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Geometrie