Mehrdimensionale Analysis

Die mehrdimensionale Analysis ist die Verallgemeinerung der (eindimensionalen) Analysis.
Dabei werden Abbildungen zwischen höherdimensionalen euklidischen Räumen betrachtet:
f:Rn→Rmf: \mathbb{R}^n \rightarrow \mathbb{R}^m
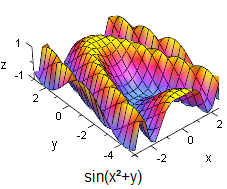
BspMA.png
Als Beispiel für eine Funktion f:R2→Rf:\mathbb{R}^2 \rightarrow \mathbb{R}, die dreidimensional darstellbar und dadurch vorstellbar ist, diene
z:=f(x,y):=sin⁡(x2+y) z:= f(x,y) := \sin(x^2+y)
Hier wird ein zweidimensionaler Raum auf einen eindimensionalen Raum abgebildet. Abbildungen zwischen Räumen höherer Dimension entzieht sich im allgemeinen unser Anschauung und können nicht mehr durch Grafiken wie die nebenstehende veranschaulicht werden.
Einen Spezialfall - der in der Vektoranalysis untersucht wird - stellen Abbildungen von und in den R3\R^3 dar, wo die Argumente oder Bilder Vektoren sind.

Inhalt

 
 

Es ist unglaublich, wie unwissend die studirende Jugend auf Universitäten kommt, wenn ich nur 10 Minuten rechne oder geometrisire, so schläft 1/4 derselben sanft ein.

Georg Christoph Lichtenberg

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung